静止于匀角速转动参考系中的物体,在此匀角速转动参考系中观察,必须附加惯性离心力,才能用牛顿定律解释它的静止状态。如果物体相对于匀角速转动参考系有运动,要在此匀角速转动参考系中应用牛顿定律,必须附加惯性力:
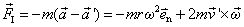
式中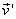 是物体相对于匀角速转动参考系的速度。第一项就是前面介绍的惯性离心力。第二项是另一个惯性力,叫科里奥利力,它的方向与物体相对于运动速度方向垂直。 是物体相对于匀角速转动参考系的速度。第一项就是前面介绍的惯性离心力。第二项是另一个惯性力,叫科里奥利力,它的方向与物体相对于运动速度方向垂直。
在以地面为参考系时,如果精度要求很高,则应把地球看做匀速转动参考系。在地球上静止的物体要附加一惯性离心力,在地球上运动的物体除要附加一惯性离心力外,还应附加一科里奥利惯性力。由于地球自转角速度很小,所以科里奥利力也很小。如果物体的运动速度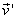 很小,科里奥利力就更小,所以常被忽略。 很小,科里奥利力就更小,所以常被忽略。
由科里奥利惯性力表达式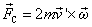 ,可以算出地面上运动的物体所受的科里奥利力。在北半球运动的物体总受到从左侧指向右侧的力,如图(a),因此北半球河床的右岸受到的冲刷较厉害。另外科里奥利力还使流动的大气形成旋风,如图(c),沿着赤道的信风,如图(b)也是科里奥利力作用的结果。 ,可以算出地面上运动的物体所受的科里奥利力。在北半球运动的物体总受到从左侧指向右侧的力,如图(a),因此北半球河床的右岸受到的冲刷较厉害。另外科里奥利力还使流动的大气形成旋风,如图(c),沿着赤道的信风,如图(b)也是科里奥利力作用的结果。
1951年法国物理学家傅科(J.B.L. Foucault,1819—1868)在巴黎巨神殿的大圆屋顶下做了著名的傅科摆实验,证明了地球是个转动的非惯性系。他把一质量为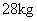 的铁球系于于 的铁球系于于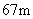 长的细铁丝下。实验发现单摆摆动面发生转动,从上往下看是顺时针方向的。 长的细铁丝下。实验发现单摆摆动面发生转动,从上往下看是顺时针方向的。
在下面的动画中一个小球在一转动的圆盘上滚动的情形很好的演示了科里奥利力的作用。
(请参阅 http://ww2010.atmos.uiuc.edu/(Gh)/guides/mtr/fw/crls.rxml)
落体偏东 |