|
现在讨论时钟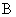 处于加速状态的第二阶段,在这一阶段,由 处于加速状态的第二阶段,在这一阶段,由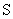 系所得的时间间隔为 系所得的时间间隔为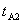 ,相应地在 ,相应地在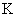 系中的时间间隔为 系中的时间间隔为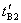 ,由于在惯性系 ,由于在惯性系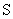 中,时钟 中,时钟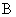 所走的每一小段距离(充分小)范围内可对应一瞬时惯性系,即加速参考系 所走的每一小段距离(充分小)范围内可对应一瞬时惯性系,即加速参考系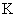 可分解为许多个瞬时惯性系,每一瞬时惯性系与 可分解为许多个瞬时惯性系,每一瞬时惯性系与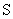 系相对应,都存在间隔不变性,即 系相对应,都存在间隔不变性,即
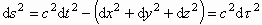
式中,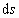 为间隔, 为间隔,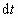 为 为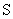 系中时钟 系中时钟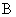 走 走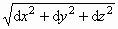 距离所用的时间, 距离所用的时间,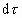 为相应的瞬时惯性系中所记下的时间间隔(固有时),而 为相应的瞬时惯性系中所记下的时间间隔(固有时),而
即瞬时惯性系(或时钟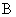 )对 )对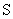 系的速度大小,于是得 系的速度大小,于是得
而
请注意,式(4-4-5)中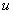 为变量,其变化范围从0到 为变量,其变化范围从0到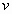 。很明显,由式(4-4-5)与式(4-4-6)对比,得 。很明显,由式(4-4-5)与式(4-4-6)对比,得
应当指出,在惯性系中观察时,加速或减速过程对时钟速率不产生影响,这已被许多实验所证实,所以式(4-4-4)和式(4-4-6)是正确的。
显然,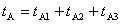 , ,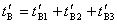 ,所以 ,所以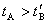
很容易做到,使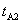 、 、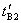 远比 远比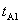 、 、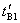 为小,以及 为小,以及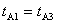 、 、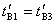 。则有 。则有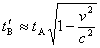 ,如果取 ,如果取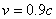 ,当 ,当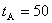 年时, 年时,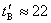 年。这就是说,当飞船的宇宙航行速度大小为 年。这就是说,当飞船的宇宙航行速度大小为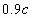 时,如果留在地球上的甲过了50年,则飞船上的乙却只过了22年。 时,如果留在地球上的甲过了50年,则飞船上的乙却只过了22年。
需要说明的是:为了更有说服力,还应讨论在时钟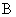 静止的参考系上观察时钟 静止的参考系上观察时钟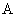 的运动,这必然遇到在非惯性系 的运动,这必然遇到在非惯性系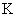 上观察时钟 上观察时钟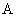 的运动,这已超出狭义相对论的范围,必须用广义相对论来处理。 的运动,这已超出狭义相对论的范围,必须用广义相对论来处理。
如图4-16所示,第一阶段是在惯性系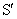 上观察时钟 上观察时钟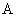 的运动,第三阶段是在惯性系 的运动,第三阶段是在惯性系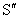 上观察时钟 上观察时钟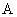 的运动。只有第二阶段是在非惯性系 的运动。只有第二阶段是在非惯性系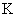 上观察时钟 上观察时钟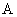 的加速运动。 的加速运动。
在第一阶段和第三阶段,时钟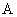 为一个运动的时钟,由各惯性系的等价性,可得 为一个运动的时钟,由各惯性系的等价性,可得
由此可见,在第一、三阶段,时钟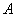 所记录的时间间隔都比时钟 所记录的时间间隔都比时钟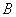 所记录的时间间隔小,这是合理的。关键问题是在第二阶段,根据广义相对论,可证明在此阶段内时钟 所记录的时间间隔小,这是合理的。关键问题是在第二阶段,根据广义相对论,可证明在此阶段内时钟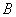 所记录的时间间隔比时钟 所记录的时间间隔比时钟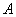 所记录的时间间隔小得多。总计之后,仍可得到 所记录的时间间隔小得多。总计之后,仍可得到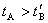 的结论。 的结论。
|