我们选一个边长分别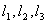 为的长方形容器〔图5-2),并设容器中有 为的长方形容器〔图5-2),并设容器中有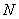 个同类气体的分子,作不规则的热运动,每个分子的质量都是 个同类气体的分子,作不规则的热运动,每个分子的质量都是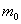 。
后,再回到 。
后,再回到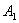 面。在与 面。在与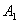 面作连续两次碰撞之间,由于分子a在 面作连续两次碰撞之间,由于分子a在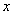 方向的速度分量 方向的速度分量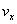 的大小不变,而在 的大小不变,而在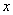 方向上所经过的路程是 方向上所经过的路程是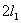 ,因此所需时间为 ,因此所需时间为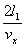 。在单位时间内,分子a就要与 。在单位时间内,分子a就要与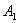 面作不连续的碰撞共 面作不连续的碰撞共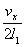 次。因为图5-2每碰撞一次,分子a作用在 次。因为图5-2每碰撞一次,分子a作用在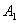 面上的冲量是 面上的冲量是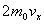 ,所以,在单位时间内,分子a作用在 ,所以,在单位时间内,分子a作用在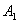 面上的冲量总值也就是作用在 面上的冲量总值也就是作用在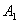 面上的力,其大小为 面上的力,其大小为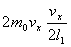 。 。
从以上讨论可知,每一分子对器壁的碰撞以及作用在器壁上的力是间歇的、不连续的。但是,事实上容器内所有分子对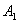 面都在碰撞,使器壁受到一个连续而均匀的压强,正与密集的雨点打到雨伞上,我们感到一个均匀的作用力相似。 面都在碰撞,使器壁受到一个连续而均匀的压强,正与密集的雨点打到雨伞上,我们感到一个均匀的作用力相似。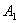 面所受的平均力 面所受的平均力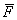 的大小应该等于单位时间内所有分子与 的大小应该等于单位时间内所有分子与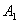 面碰撞时所作用的冲量的总和,即 面碰撞时所作用的冲量的总和,即
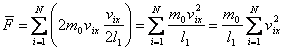
式中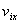 是第 是第 个分子在 个分子在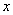 方向上的速度分量。按压强定义得 方向上的速度分量。按压强定义得
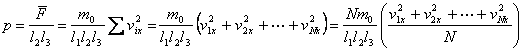
式中括弧内的量是容器内 个分子沿 个分子沿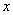 方向速度分量平方的平均值,可写作 方向速度分量平方的平均值,可写作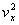 。又因气体的体积为 。又因气体的体积为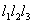 ,单位体积内的分子数 ,单位体积内的分子数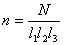 ,所以上式可写作 ,所以上式可写作
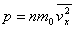
根据统计假设,沿各个方向速度分量平方的平均值应该相等,
即 ,又因为 ,又因为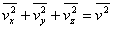 ,所以 ,所以
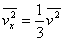
此处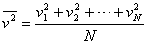 为 为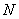 个分子的速度平方的平均值。考虑到分子的平均平动动能 个分子的速度平方的平均值。考虑到分子的平均平动动能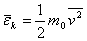 ,代人上式得 ,代人上式得
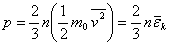
由上式可知,气体作用在器壁上的压强,既和单位体积内的分子数有关,又和分子的平均平动动能有关。由于分子对器壁的碰撞是断断续续的,分子给予器壁的冲量是有起伏的。所以,压强是个统计平均量。在气体中,分子数密度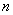 也有起伏,所以 也有起伏,所以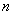 也是个统计平均量。上式给出了三个统计平均量 也是个统计平均量。上式给出了三个统计平均量 、 、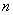 和 和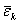 之间的关系,是个统计规津,而不是力学规律。 之间的关系,是个统计规津,而不是力学规律。 |