设每个分子的质量是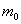 ,则气体的摩尔质量 ,则气体的摩尔质量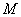 与 与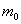 之间应有关系 之间应有关系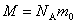 ,而气体质量为 ,而气体质量为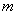 时的分子数为 时的分子数为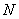 ,所以 ,所以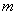 与 与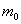 之间也有关系 之间也有关系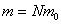 。把这两个关系代人理想气体状态方程 。把这两个关系代人理想气体状态方程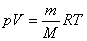 ,消去 ,消去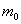 后,理想气体状态方程可写作 后,理想气体状态方程可写作
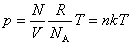
式中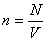 为单位体积中的分子数,称为分子数密度; 为单位体积中的分子数,称为分子数密度;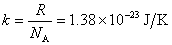 ,称为玻耳兹曼(L.Boltzman)常量。 将上式和气体压强公式 ,称为玻耳兹曼(L.Boltzman)常量。 将上式和气体压强公式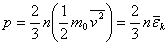 相比较,得 相比较,得
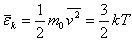
上式是宏观量温度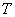 与微观量 与微观量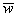 的关系式,说明分子的平均平动动能仅与温度成正比。即气体的温度是气体分子平均平动动能的量度。由此可见,温度是大量气体分子热运动的集体表现,具有统计的意义;对个别分子,说它有温度是没有意义的。 的关系式,说明分子的平均平动动能仅与温度成正比。即气体的温度是气体分子平均平动动能的量度。由此可见,温度是大量气体分子热运动的集体表现,具有统计的意义;对个别分子,说它有温度是没有意义的。
根据上述结论,在一定的温度下,各种气体分子的平均平动动能都相等。按照这个观点,热力学温度零度将是理想气体分子热运动停止时的温度,然而实际上分子运动是永远不会停息的。热力学温度零度也是永远不可能达到的,而且近代理论指出,即使在热力学温度零度时,组成固体点阵的粒子也还保持着某种振动的能量,叫做零点能量。至于气体,则在温度未达到热力学温度零度以前,已变成液体或固体,上述公式也早就不能适用。
皮兰(J.B.Perrin)对布朗运动的研究,进一步证实浮悬在温度均匀的液体中的不同微粒,不论其质量的大小如何,它们各自的平均平动动能都相等。气体分子的运动情况和浮悬在液体中的布朗微粒相似,所以皮兰的实验结果,也可作为在同一温度下各种气体分子的平均平动动能都相等的一个证明。 |