|
在常温下,气体分子以每秒几百米的平均速率运动着。据此推断,似乎气体中的一切过程都应在极短时间内完成。但实标情况并非如此,气体的混合(扩散过程)进行得相当慢,经验告诉我们,打开汽油瓶以后,汽油味要经过几分钟的时间才能传过几米的距离。
实际上,在分子由一处(如图5-6中的A点)移至另一处(如B点)的过程中,它要不断地与其他分子碰撞,这就使分子沿着迂回的折线前进。气体的扩散、热传导过程等进行的快慢都取决于分子相互碰撞的频繁程度。
气体分子在运动中经常与其他分子碰撞,在任意两次连续的碰撞之间,一个分子所经过的自由路程的长短显然不同,经过的时间也是不同的。我们不可能也没有必要一个个地求出这些距离和时间来,但是我们可以求出在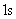 内一个分子和其他分子碰撞的平均次数,以及每两次连续碰撞间一个分子自由运动的平均路程。前者叫做分子的平均碰撞次数或平均碰撞频率,以 内一个分子和其他分子碰撞的平均次数,以及每两次连续碰撞间一个分子自由运动的平均路程。前者叫做分子的平均碰撞次数或平均碰撞频率,以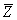 表示,后者叫做分子的平均自由程,以 表示,后者叫做分子的平均自由程,以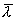 表示。 表示。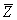 和 和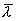 的大小反映了分子间碰撞的频繁程度。 的大小反映了分子间碰撞的频繁程度。 |