已知电荷分布,求电势的方法有两种:一种是若已经知道了电场强度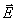 的分布函数,那么就可以直接应用电势的定义式(7-28)作一积分运算(但电荷分布到无限远时,则不能取无限远为零电势点,见例题7-14);另一种方法是根据电势的叠加原理求出任意电荷分布的电势。下面就后一种方法作进一步的讨论。 的分布函数,那么就可以直接应用电势的定义式(7-28)作一积分运算(但电荷分布到无限远时,则不能取无限远为零电势点,见例题7-14);另一种方法是根据电势的叠加原理求出任意电荷分布的电势。下面就后一种方法作进一步的讨论。
(1)点电荷电场中的电势
设点电荷q静止于坐标系的原点,则距q为r处P点的电势,由式(7-28)和式(7-27)可知是
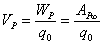
由式(7-23)可知
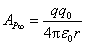
将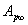 代入上式,求得 代入上式,求得
由此可见,在点电荷周围空间任一点的电势与该点离点电荷q的距离r成反比。如果q是正的,各点的电势是正的,离点电荷愈远处电势愈低,在无限远处电势为零;如果q是负的,各点的电势也是负的,离点电荷愈远处电势愈高,在无限远处电势最大为零值。
(2)点电荷系电场中的电势
如果电场由n个点电荷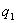 、 、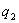 、…、 、…、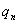 所激发,某点P的电势由电场强度叠加原理可知为 所激发,某点P的电势由电场强度叠加原理可知为
式中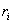 是P点离开点电荷 是P点离开点电荷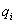 的相应的距离。上式表明,在点电荷系的静电场中,某点的电势等于每一个点电荷单独在该点所激发的电势的代数和。电势的这个性质称为电势的叠加原理。 的相应的距离。上式表明,在点电荷系的静电场中,某点的电势等于每一个点电荷单独在该点所激发的电势的代数和。电势的这个性质称为电势的叠加原理。
(3)连续分布电荷电场中的电势
如果静电场是由电荷连续分布的带电体所激发,要求某点P的电势,可以根据电势叠加原理将带电体分成许多电荷元dq,每个电荷元在P点的电势按式(7-33)计算,那么整个带电体在P点的电势为
根据电荷是体分布、面分布或线分布等不同情况将积分遍及整个带电体。因为电势是标量,这里的积分是标量积分,所以电势的计算比电场强度的计算较为简便。
应该注意,在式(7-32)、式(7-33)和式(7-34)的计算式中,电荷都是分布在有限区域内的,并且是选择无限远处为电势的零点.但当激发电场的电荷分布延伸到无限远时,不宜把电势的零点选在无限远处,否则将导致场中任一点的电势值为无限大,这时只能根据具体问题,在场中选某点为电势的零点,下例就是这种情况。 |






