电场强度和电势都是用来描述同一静电场中各点性质的物理量,两者之间有密切的关系。式(7-28)和式(7-29)指明两者之间的积分形式关系,即已知道电场强度分布可以通过空间积分来求得电势。本节将着重研究它们之间的微分关系。
设在任意静电场中,取两个十分邻近的等势面1和2(图7-19),电势分别为V 和 ,并设dV>0。假定一个正的试探电荷 ,并设dV>0。假定一个正的试探电荷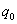 从等势面1上的 从等势面1上的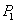 点经 点经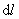 到达等势面2上 到达等势面2上 点,那么电场力所作的功是 点,那么电场力所作的功是
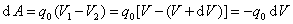
按公式(7-34),这个功又可以写作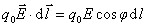 ,j是 ,j是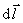 与等势面1法线方向 与等势面1法线方向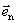 之间的夹角,所以 之间的夹角,所以

整理后有

上式左边正是电场强度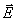 在 在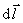 方向上的分量 方向上的分量 ,这样 ,这样
它表明电场强度在任一方向上的分量等于该方向电势的变化率的负值。将上式应用于等势面1上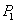 点法线方向,即 点法线方向,即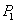 点(电势V )经 点(电势V )经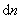 变化到 变化到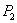 点(电势 点(电势 ),有
由于 ),有
由于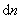 总是小于 总是小于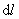 的,所以 的,所以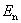 为 为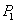 点最大的电势空间变化率。于是把沿法线 点最大的电势空间变化率。于是把沿法线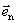 方向的这个电势变化率定义为 方向的这个电势变化率定义为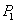 点处的电势梯度矢量,通常记作grad V(“grad”是英语梯度一词“gradient”的缩写,grad V 读做“V 的梯度”。 点处的电势梯度矢量,通常记作grad V(“grad”是英语梯度一词“gradient”的缩写,grad V 读做“V 的梯度”。
如前所述,电场线的方向,亦即电场强度的方向,恒垂直于等势面,而且指向电势降落的方向。 所以(7-36)式的 即为 即为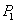 点的电场强度 点的电场强度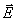 值,它的方向与 值,它的方向与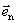 的方向相反(如图7-19中所示),这样
式中的负号正是说明 的方向相反(如图7-19中所示),这样
式中的负号正是说明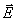 的方向与 的方向与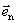 的方向是相反的。 的方向是相反的。
在直角坐标系中,电势是空间坐标的函数V(x,y,z),把(7-35)式应用于它的三个坐标方向,就可得到电场强度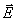 沿这三个方向的分量分别为 沿这三个方向的分量分别为 |
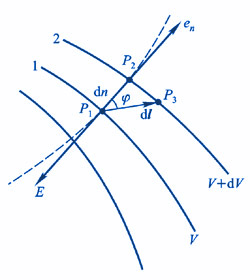 图 7-19 电势梯度矢量和电场强度的关系
图 7-19 电势梯度矢量和电场强度的关系 |
因此,在直角坐标系中电场强度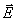 可写成
可见电势梯度grad V 在直角坐标系中可写成
式中的 可写成
可见电势梯度grad V 在直角坐标系中可写成
式中的 分别是电势梯度在x轴、y轴、z轴三个方向的分量。 分别是电势梯度在x轴、y轴、z轴三个方向的分量。
电势梯度的单位是V/m,所以电场强度也常用这一单位。
电场强度和电势梯度之间的关系式,在实际应用中很重要。 因为电势是标量,一般说来标量计算比较简便,在求得电势分布后,只需进行空间导数运算便可算出电场强度的各个分量,这样就可以避免较复杂的矢量运算。下面我们用几个例题来说明如何由电势分布来计算电场强度。
|