当带电导体处于静电平衡状态时,导体上电荷分布的规律可以从高斯定理直接推出,考虑一个任意形状的实心导体,如图7-23(a)所示。在导体内任取一点P,围绕它任作一闭合曲面S,因为在这个封闭合面上任一点的电场强度都等于零,根据高斯定理可知,通过这一封闭曲面的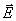 通量等于零,因此在这一封闭曲面内没有净电荷。由于点P是任意的,上述结论对于导体内部任一点都是正确的。另一方面,如果封闭曲面内有空腔存在[图7-23(b)],而且在空腔内没有其他带电体,那么同样的道理,不仅导体内部没有净电荷,而且在空腔的内表面上处处也不能有净电荷存在。所以我们可作如下的结论:当带电导体处于静电平衡状态时,导体内部处处没有净电荷存在,电荷只能分布于导体的外表面上。 通量等于零,因此在这一封闭曲面内没有净电荷。由于点P是任意的,上述结论对于导体内部任一点都是正确的。另一方面,如果封闭曲面内有空腔存在[图7-23(b)],而且在空腔内没有其他带电体,那么同样的道理,不仅导体内部没有净电荷,而且在空腔的内表面上处处也不能有净电荷存在。所以我们可作如下的结论:当带电导体处于静电平衡状态时,导体内部处处没有净电荷存在,电荷只能分布于导体的外表面上。
但如果在导体腔中有一电荷为q的带电体,如图7-23(c)所示,这时由于静电感应,在导体静电平衡时,可以证明导体腔的内表面上出现和带电体所带电荷等值异号的感应电荷-q,而在腔体外表面上出现和带电体所带电荷等值同号的+q感应电荷,此时导体内其他地方仍没有净电荷。
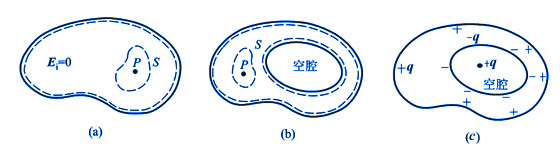 图 7-23 论证导体静电平衡时电荷只能分布在导体的表面上
图 7-23 论证导体静电平衡时电荷只能分布在导体的表面上 |
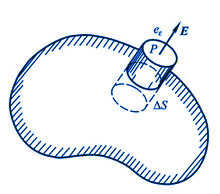 图 7-24 带电导体表面附近的电场强度和该表面处电荷面密度的关系
图 7-24 带电导体表面附近的电场强度和该表面处电荷面密度的关系 |
由高斯定理还可以求出导体表面附近的电场强度与该表面处电荷面密度的关系。在导体表面外无限靠近表面处任取一点P,过P作一个很小极薄的扁平圆柱形闭合面,使圆柱的轴线垂直于导体表面,它的上下两个底面与导体表面平行,底面积为ΔS,下底面深入在导体内(图7-24)。由于导体内部电场强度为零,导体表面的电场强度与表面垂直,圆柱面的侧面与电场强度方向平行,所以通过下底面和侧面的 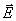 通量都为零,通过该闭合曲面的总 通量都为零,通过该闭合曲面的总 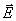 通量就等于通过圆柱面上底面的 通量就等于通过圆柱面上底面的 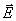 通量,应用高斯定理得 通量,应用高斯定理得
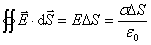
则 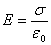
将上式的结果写成矢量式为
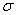 是导体表面P 点处的电荷面密度, 是导体表面P 点处的电荷面密度, 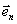 是导体表面的法向单位矢量。上式表明带电导体表面附近的电场强度与该表面的电荷面密度成正比,电场强度方向垂直于表面,这一结论对于孤立导体(孤立导体是指远离其他物体的导体,因而其他物体对它的影响可以忽略不计)或处在外电场中的任意导体都普遍适用。但在理解式(7-42)时必须注意,导体表面附近的电场强度 是导体表面的法向单位矢量。上式表明带电导体表面附近的电场强度与该表面的电荷面密度成正比,电场强度方向垂直于表面,这一结论对于孤立导体(孤立导体是指远离其他物体的导体,因而其他物体对它的影响可以忽略不计)或处在外电场中的任意导体都普遍适用。但在理解式(7-42)时必须注意,导体表面附近的电场强度 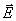 不单是由该表面处的电荷所激发,它是导体面上所有电荷以及周围其他带电体上的电荷所激发的合电场强度,外界的影响已在 不单是由该表面处的电荷所激发,它是导体面上所有电荷以及周围其他带电体上的电荷所激发的合电场强度,外界的影响已在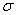 中体现出来。例如,一个半径为R的孤立导体球,带有电荷量q,则在紧靠球外侧某点处的电场强度的大小为 中体现出来。例如,一个半径为R的孤立导体球,带有电荷量q,则在紧靠球外侧某点处的电场强度的大小为 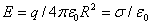 ,显然,E是整个球面上的电荷所激发的。如果在这导体球邻近再放置一个电荷量为 ,显然,E是整个球面上的电荷所激发的。如果在这导体球邻近再放置一个电荷量为 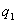 的平板(如图7-22所示),这时该点的电场强度就由 的平板(如图7-22所示),这时该点的电场强度就由 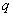 、 、 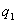 以及 以及 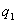 在球面上的感应电荷共同激发,在该点的电场强度(设为 在球面上的感应电荷共同激发,在该点的电场强度(设为 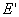 )和靠近它的球面上的电荷面密度(设为 )和靠近它的球面上的电荷面密度(设为 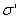 )都有了变化,尽管如此,它们仍满足 )都有了变化,尽管如此,它们仍满足 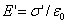 的关系。 的关系。
最后,我们来简单讨论一下电荷在导体表面上分布的规律。导体表面虽是一等势面,但其电荷面密度不一定处处相同。一般说来,电荷在导体表面上的分布不但和导体自身的形状有关,还和附近其他带电体及其分布有关。对于孤立的带电导体来说,电荷在其表面上的分布却由导体表面的曲率决定,即在导体表面凸出而尖锐的地方(曲率较大),电荷面密度较大;在表面平坦的地方(曲率较小),电荷面密度较小;在表面凹进去的地方(曲率为负),电荷面密度更小。只有孤立球形导体,因各部分的曲率相同,球面上的电荷分布才是均匀的。
|
 图 7-25 电荷面密度与曲率半径成反比
图 7-25 电荷面密度与曲率半径成反比 |
上面所得结论在生产技术上十分重要。对于具有尖端的带电导体,由于尖端处电荷密度极高,其周围的电场强度特别强,空气中的残留离子受到这个强电场的作用与空气其他分子剧烈碰撞而产生大量的离子。其中和导体上电荷异号的离子,被吸引到尖端上,与导体上的电荷相中和,而和导体上电荷同号的离子,则被排斥而离开尖端。这种使得空气被“击穿”而产生的放电现象称为尖端放电。避雷针就是根据尖端放电的原理制造的,当雷电发生时,利用尖端放电原理使强大的放电电流从和避雷针连接并接地良好的粗导线中流过,从而避免了建筑物遭受雷击的破坏。
尖端放电现象在高压输电网的导线上及一些高压设备中也常出现(又称电晕),造成电能的损失。在出现电晕现象的电场中,不仅有离子在运动,大气中的中性微尘由于有离子附着在它们上面而带电,也能在电场中作定向运动。“静电喷漆”就是利用电晕原理使漆雾微粒带电而喷射到工件上。在工厂中也利用这个原理制成除尘器来除去大气中的有害粉尘。静电的应用很广泛,除上述例举的应用之外,例如范德格拉夫静电起电机、静电复印等,此处仅介绍了几例。
 图1 避雷针
图1 避雷针 |
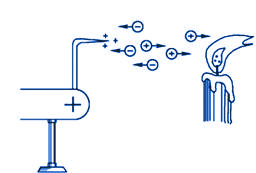 图2 尖端放电实验
图2 尖端放电实验 |
|






