1.电流 电流密度
通常,电流是电荷作定向运动形成的。电荷的携带者叫载流子,金属导体中的载流子是大量可以作自由运动的电子;半导体中的载流子是电子和带正电的“空穴”;电解液中的载流子是其中的正负离子,这些载流子形成的电流叫做传导电流。
电流的强弱用电流强度这一物理量来描述,用符号I表示。电流强度定义为在单位时间内通过导体截面的电荷量
如果电流的大小和方向不随时间而变化,则称为恒定电流(俗称直流)。由于历史的原因,规定正电荷定向运动的方向为电流的方向。电流是标量,所谓电流的方向是指电流沿导体循行的指向。在国际单位制中规定电流为基本量,单位是安培。
电流强度I虽能描写电流的强弱,但它只能反映通过导体截面的整体电流特征,并不能说明电流通过截面上各点的情况。在实际问题中,常会遇到电流在粗细不均或材料不均匀、甚至大块金属中通过的情况,这时,如果在单位时间内通过某一根粗细不均的导线各截面的的电流强度I相同,那么在导线内部不同点的电流情况将不相同。因此,电流强度I这个物理量不能细致反映出电流在导体中的分布。图8-1分别画出了在导线和大块导体中的电流分布情况。为了细致地描述导体内各点电流分布的情况,必须引入一个新的物理量叫电流密度,电流密度是矢量,用符号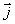 表示。电流密度矢量的方向与该点正电荷运动的方向一致,大小等于通过垂直于电流方向的单位面积的电流,记作 表示。电流密度矢量的方向与该点正电荷运动的方向一致,大小等于通过垂直于电流方向的单位面积的电流,记作
电流密度是空间位置的矢量函数,它能精确地描述导体中电流分布的情况。
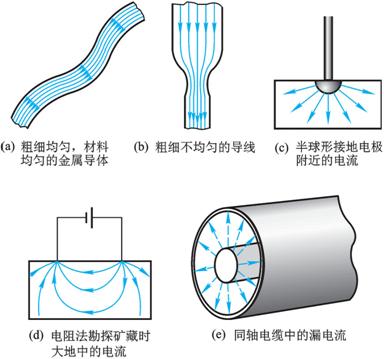
图 8-1 在导线和大块导体中的电流分布情况 |
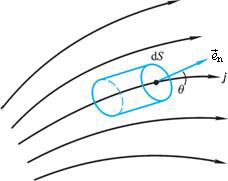
图 8-2 电流 I与电流密度 j关系的推导 |
在一般情况下,截面元dS法线的单位矢量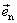 与该点电流密度 与该点电流密度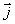 之间有一夹角θ,如图8-2所示。此时通过任一截面的电流为 之间有一夹角θ,如图8-2所示。此时通过任一截面的电流为
在国际单位制中,电流密度的单位为A/m2。
2.电源的电动势
将一个电势较高带正电的导体A同一个电势较低带负电的导体B用导线连接起来,在连接的瞬间,正电荷将沿着存在电场的导线从高电势的导体A流向电势低的导体B,形成短暂的电流(实际上在导线中做宏观定向运动的是自由电子)。随着电荷的不断迁移,两导体A和B间的电势差逐渐减小,导线中的电流也随着减小,直至A和B的电势相等,金属导线内的场强为零,电流也随之停止。 这时,整个导体组达到静电平衡,所以,仅仅依靠短暂的静电场,不可能使金属导体内的自由电子保持持久的宏观定向运动。为了在导线中维持恒定的电流,必须把达到B的正电荷不断地输送到导体A上,保持导体A和导体B间的电势差不变,使导线内的电流得以循环流动。这就需要一个能提供性质与静电力很不相同的“非静电力”把正电荷从低电势的B移向高电势的A的装置,这个装置称为电源(图8-3)。电源的作用如同人造瀑布后的抽水机一样,水依靠重力场的作用从高处奔腾而下,但不能仍依靠重力作功把水送到高端,而必须借助非重力场的能量作功才能把水抽上去,形成循环瀑布。
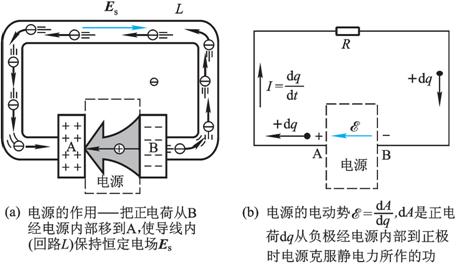
图 8-3 |
因此,电源是把其他形式能量转化为电势能的装置。各种形式的能量都可转化为电势能,所以有各种各样的电源。例如,有化学电池、发电机、热电偶、硅(硒)太阳电池、核反应堆等电源,它们分别是把化学能、机械能、热能、太阳能、核能变为电势能的装置。为了描述电源内能移动电荷的“非静电力”作功的本领,引入电动势这个物理量,并定义为
即电源的电动势等于电源把单位正电荷从负极经电源内移到正极所作的功。 电动势是标量,但习惯上为便于应用,常规定电动势的指向为自负极经电源内到正极。沿着电动势的指向,电源将提高正电荷的电势能。 电动势的单位和电势相同,也是J/C,即V。
非静电力移动电荷作功,可以设想在电源内存在一“非静电性场”,与静电场的定义类似,单位正电荷受到的非静电力定义为“非静电力场的场强”,记作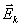 。因此非静电性场把单位正电荷从负极经电源内移到正极所作的功就可以表达为 。因此非静电性场把单位正电荷从负极经电源内移到正极所作的功就可以表达为
由于在如图8-3所示的闭合电路中,电源外 =0;或者,在某个闭合电路中处处存在 =0;或者,在某个闭合电路中处处存在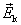 而无所谓“电源内部”和“电源外部”,那么可以把上式扩展到整个闭合电路,即电动势可表为“非静电性场的场强 而无所谓“电源内部”和“电源外部”,那么可以把上式扩展到整个闭合电路,即电动势可表为“非静电性场的场强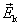 ” 沿整个闭合电路的环流 ” 沿整个闭合电路的环流
这就是说,“非静电性场的场强”沿整个闭合电路的环流不等于零,而等于电源的电动势。这是非静电性场的场强与静电场的区别,后者的环流服从场强的环流定理。
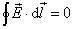
3.欧姆定律
(1)一段含源电路的欧姆定律
在中学物理中我们已经学习过欧姆定律,这个定律告诉我们,通过一段导体的电流与导体两端的电势差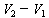 成正比,可以表达为 成正比,可以表达为
式中的比例系数R是该段导体的电阻,它与导体材料有关。实验指出,对于给定材料的导体,其电阻正比于长度l,反比于截面积S,写作
式中的比例系数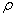 称作电阻率,它的倒数 称作电阻率,它的倒数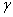 ( (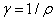 )叫做电导率,它们均与导体材料及温度有关。在国际单位制中,电阻率的单位为Ω·m,电导率的单位为S/m(电阻的单位是欧姆,用符号Ω表示,S是电阻的倒数电导的单位西门子的符号)。 )叫做电导率,它们均与导体材料及温度有关。在国际单位制中,电阻率的单位为Ω·m,电导率的单位为S/m(电阻的单位是欧姆,用符号Ω表示,S是电阻的倒数电导的单位西门子的符号)。
在实际电路中,我们遇到的大多数电路都是由电阻和电源连接成的闭合电路,如图8-4所示的由一个电动势为ε的电源和一个电阻R组成的最简单闭合电路,r是电源的内阻,导线的电阻可忽略不计。在电源外电路,电流从电源的正极(高电势)经电阻元件(称作负载)流向电源的负极(低电势),即在电阻上产生了电势降;在电源内部,由于非静电力作功,电流从电源负极回到正极,产生了电势升。绕行一周后,各部分的电势变化总和为零,即电势降等于电势升
由欧姆定律,在负载电阻R上的电势降(电压)和电源内的电阻r上的电势降分别是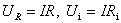 代入上式,得 代入上式,得
上式表示闭合电路中的电流等于电源的电动势除以电路的总电阻,称作闭合电路的欧姆定律。上式可推广到由若干个电源和电阻组成的电路,则回路的电流为
这就是闭合电路欧姆定律的一般形式,式中的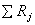 和 和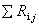 分别是电路总负载电阻和电源内阻之和。在有多个电动势的情况下,式中电动势的正负取向可作如下规定:先任意设定电路中的电流方向,如果电动势的指向和电流方向相同,该电动势为正 分别是电路总负载电阻和电源内阻之和。在有多个电动势的情况下,式中电动势的正负取向可作如下规定:先任意设定电路中的电流方向,如果电动势的指向和电流方向相同,该电动势为正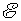 ,相反则是负 ,相反则是负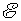 。依照这样的约定,图8-5所示的电路的电流为 。依照这样的约定,图8-5所示的电路的电流为
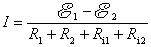
计算结果为负时,表明电流流向和设定绕行方向相反。
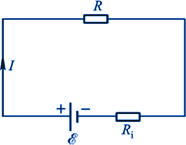
图 8-4 简单的闭合电路 |
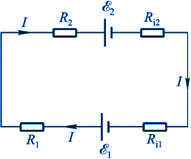
图 8-5 多个电源和电阻的电路 |
在电路计算中,我们还经常遇到在整个电路中抽出一段包含几个电源而且各部分电流不相等的电路的端电势差计算问题。如图8-6的电路,应用前述电势变化的计算方法,可得A,B两点之间有电势差为
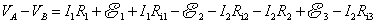
可写成一般形式
上式称为一段含源电路的欧姆定律。应用这一公式时,右边各项选取正负号的规则如下:先任意设定电路顺序方向,如果电阻中的电流流向与设定电路顺序方向相同,则该电阻上的电势降取“+”号,反之则取
“-”号;如果电动势的指向和设定的顺序方向相同,该电动势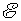 取“+”号,反之则取“-”号。 取“+”号,反之则取“-”号。
(2)欧姆定律的微分形式
式(8-7)形式的欧姆定律反映了一段有限大小导体的导电规律,称作是欧姆定律的积分形式。但从图8-1可以看到,在一段导体内各点的电流常常并非总是均匀的,为了更精细地描绘出导体的导电情况,我们将从场的观点导出欧姆定律的微分形式,它将反映出导体中逐点的导电规律。 |
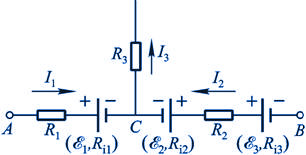
图 8-6一段复杂的含源电路 |
在宏观上看,导体中的电流是导体两端有一定的电势差产生的。现在导体中沿电流方向取一极小的直圆柱体(图8-7),其截面积大小为dS,柱体长度为dl,两端的电势分别为V和(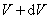 ,假定这端圆柱体的电阻为R,根据欧姆定律,通过该小圆柱体的电流是 ,假定这端圆柱体的电阻为R,根据欧姆定律,通过该小圆柱体的电流是
将电阻计算的(8-9)式应用于所讨论的小圆柱体,则小圆柱体的电阻为 |
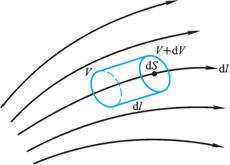
图 8-7 欧姆定律的微分形式的推导
|
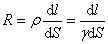
将上式代入(8-12)式,通过该小圆柱体的电流改写为
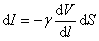
或
上式左边是电流密度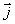 ,右边电势梯度的负值正是电场强度 ,右边电势梯度的负值正是电场强度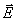 ,考虑到在导体中 ,考虑到在导体中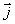 与 与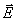 方向相同,所以可以将(8-13)式表达为矢量关系 方向相同,所以可以将(8-13)式表达为矢量关系
式(8-14)称为欧姆定律的微分形式,它表明导体中任一点处电流密度与电场强度之间的关系。式中的γ表征了导体中该点处的导电性质,在均匀的导电材料中,当场强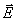 的量值增加或减小时,相应的 的量值增加或减小时,相应的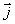 的量值也正比地改变。当材料不均匀或温度不均匀时,导体中各点处的γ值并不一样,因此即使各点 的量值也正比地改变。当材料不均匀或温度不均匀时,导体中各点处的γ值并不一样,因此即使各点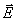 的大小和方向都不改变时,各点因γ值不同 的大小和方向都不改变时,各点因γ值不同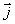 仍可能发生变化。在可变电场中,式(8-14)也是成立的。总之,欧姆定律的微分形式是用场的观点表述了大块导体中的电场(以电场强度 仍可能发生变化。在可变电场中,式(8-14)也是成立的。总之,欧姆定律的微分形式是用场的观点表述了大块导体中的电场(以电场强度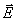 描述)和导体中的电流分布(以电流密度 描述)和导体中的电流分布(以电流密度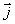 描述)之间逐点的细节的关系,它是电磁理论中反映介质的电磁性质的基本方程之一。 描述)之间逐点的细节的关系,它是电磁理论中反映介质的电磁性质的基本方程之一。 |






