1.洛伦兹力
当带电粒子沿磁场方向运动时,作用在带电粒子上的磁力为零;带电粒子的运动方向与磁场方向相垂直时,所受磁力最大,记作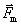 ,其值为 ,其值为
并且磁力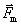 、电荷运动速度和磁感应强度 、电荷运动速度和磁感应强度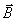 三者相互垂直。在一般情况下,如果带电粒子运动的方向与磁场方向成夹角 三者相互垂直。在一般情况下,如果带电粒子运动的方向与磁场方向成夹角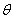 ,则所受磁力 ,则所受磁力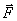 的大小为 的大小为
2.带电粒子在磁场中的运动
下面讨论带电粒子在均匀及不均匀磁场中运动的基本规律。
(1)带电粒子在均匀磁场中运动
设有一均匀磁场,磁感应强度为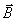 ,一电荷量为 ,一电荷量为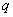 、质量为 、质量为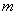 的粒子,以初速 的粒子,以初速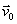 进人磁场中运动。分三种情况进行分析。 进人磁场中运动。分三种情况进行分析。
(a)如果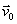 与 与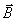 相互平行,作用于带电粒子的洛伦兹力等于零,带电粒子不受磁场的影响,进人磁场后仍作匀速直线运动。 相互平行,作用于带电粒子的洛伦兹力等于零,带电粒子不受磁场的影响,进人磁场后仍作匀速直线运动。
(b)如果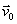 与 与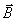 垂直,这时粒子将受到与运动方向垂直的洛伦兹力 垂直,这时粒子将受到与运动方向垂直的洛伦兹力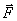 , ,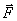 的大小为 的大小为
方向垂直于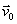 及 及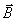 。所以粒子速度的大小不变,只改变方向。带电粒子将作匀速圆周运动,而洛伦兹力起着向心力的作用,因此 。所以粒子速度的大小不变,只改变方向。带电粒子将作匀速圆周运动,而洛伦兹力起着向心力的作用,因此
式中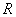 是粒子的圆形轨道半径。 是粒子的圆形轨道半径。
带电粒子绕圆形轨道一周所需的时间(周期)为
这一周期与带电粒子的运动速度无关,这一特点是后面将介绍的磁聚焦和回旋加速器的理论基础。
螺距是
式中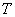 为旋转一周所用的时间。式(8-71)表明,螺距 为旋转一周所用的时间。式(8-71)表明,螺距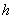 大小和平行于磁场的速度分量 大小和平行于磁场的速度分量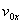 有关;而和垂直于磁场分量速度 有关;而和垂直于磁场分量速度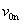 无关。 无关。
(2)带电粒子在非均匀磁场中运动
带电粒子在均匀磁场中可绕磁感应线作螺旋运动,螺旋线的半径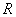 与磁感应强度 与磁感应强度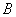 成反比,所以当带电粒子在非均匀磁场中向磁场较强的方向运动时,螺旋线的半径将随着磁感应强度的增加而不断地减小,如图8-24所示。同时,这带电粒子在非均匀磁场中受到的洛伦兹力,恒有一指向磁场较弱的方向的分力,此分力阻止带电粒子向磁场较强的方向运动。这样有可能使粒子沿磁场方向的速度逐渐减小到零,从而迫使粒子掉向反转运动。如果在一长直圆柱形真空室中形成一个两端很强、中间较弱的磁场(图8-25),那么两端较强的磁场对带电粒子的,运动起着阻塞的作用,它能迫使带电粒子局限在一定的范围内往返运动,这种装置称为磁塞。由于带电粒子在两端处的这种运动好像光线遇到镜面发生反射一样,所以这种装置也称为磁镜。在受控热核反应装置中,一般都采用这种磁场把等离子体约束在一定的范围内。 成反比,所以当带电粒子在非均匀磁场中向磁场较强的方向运动时,螺旋线的半径将随着磁感应强度的增加而不断地减小,如图8-24所示。同时,这带电粒子在非均匀磁场中受到的洛伦兹力,恒有一指向磁场较弱的方向的分力,此分力阻止带电粒子向磁场较强的方向运动。这样有可能使粒子沿磁场方向的速度逐渐减小到零,从而迫使粒子掉向反转运动。如果在一长直圆柱形真空室中形成一个两端很强、中间较弱的磁场(图8-25),那么两端较强的磁场对带电粒子的,运动起着阻塞的作用,它能迫使带电粒子局限在一定的范围内往返运动,这种装置称为磁塞。由于带电粒子在两端处的这种运动好像光线遇到镜面发生反射一样,所以这种装置也称为磁镜。在受控热核反应装置中,一般都采用这种磁场把等离子体约束在一定的范围内。
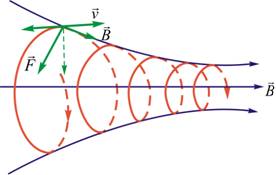
图 8-24 |
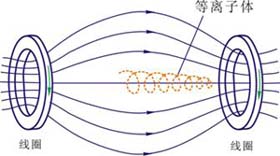
图 8-25 |
上述磁约束的现象也存在于宇宙空间。因为地球是一个磁体,磁场在两极强而中间弱。当来自外层空间的大量带电粒子(宇宙射线)进人磁场影响范围后,粒子将绕地磁感应线作螺旋运动,因为在近两极处地磁场增强,作螺旋运动的粒子将被折回,结果粒子在沿磁感应线的区域内来回振荡,形成范艾仑(J.A. Van Allen)辐射带(见图8-26),此带相对地球轴对称分布,在图中只绘出其中一支。有时,太阳黑子活动使宇宙中高能粒子剧增,这些高能粒子在地磁感应线的引导下在地球北极附近进人大气层时将使大气激发,然后辐射发光,从而出现美妙的北极光。
|
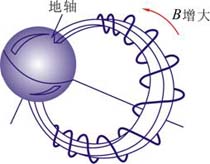
图 8-26
|
3.带电粒子在电磁场中的运动和应用
如果在空间内除了磁场外还有电场存在,那么带电粒子还要受到电场力的作用。这时,带有电荷量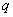 的粒子在静电场 的粒子在静电场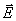 和磁场 和磁场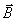 中以速度 中以速度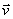 ,运动时受到的作用力将是 ,运动时受到的作用力将是
上式叫做洛伦兹关系式。当粒子的速度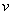 远小于光速 远小于光速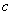 时,根据牛顿第二定律,带电粒子的运动方程(设重力可略去不计)为 时,根据牛顿第二定律,带电粒子的运动方程(设重力可略去不计)为
式中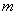 为粒子的质量, 为粒子的质量,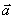 表示粒子的加速度。在一般的情况下,求解这一方程是比较复杂的。事实上,我们经常遇到利用电磁力来控制带电粒子运动的例子,所用的电场和磁场分布都具有某种对称性,这就使求解方程简便得多。下面我们讨论几种简单而重要的实例。 表示粒子的加速度。在一般的情况下,求解这一方程是比较复杂的。事实上,我们经常遇到利用电磁力来控制带电粒子运动的例子,所用的电场和磁场分布都具有某种对称性,这就使求解方程简便得多。下面我们讨论几种简单而重要的实例。
(1)磁聚焦
图8-27是磁聚焦装置的示意图,从阴极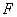 发射出来的电子束经过极板 发射出来的电子束经过极板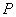 和阴极 和阴极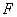 间的电压 间的电压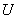 加速后,先通过一横向电场,再进人一纵向均匀磁场。通常是在一组平行板上加一幅值很小的交变电压以产生横向电场,并用一载流长螺线管得到沿轴向的均匀磁场。由于电子束受横向电场作用后稍有散开,各电子将以不同的角度(一般很小)进人磁场,所以各电子垂直磁场的速度分量不相等,电子将沿着磁感应线作不同半径的螺旋线运动,但它们平行磁场的速度分量近似相等,以致经过一个级距的运动之后,散开的电子束重又会聚于一点。如电子在磁场中运动的纵向路径长度为 加速后,先通过一横向电场,再进人一纵向均匀磁场。通常是在一组平行板上加一幅值很小的交变电压以产生横向电场,并用一载流长螺线管得到沿轴向的均匀磁场。由于电子束受横向电场作用后稍有散开,各电子将以不同的角度(一般很小)进人磁场,所以各电子垂直磁场的速度分量不相等,电子将沿着磁感应线作不同半径的螺旋线运动,但它们平行磁场的速度分量近似相等,以致经过一个级距的运动之后,散开的电子束重又会聚于一点。如电子在磁场中运动的纵向路径长度为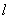 ,调节磁感应强度 ,调节磁感应强度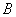 ,使比值一示 ,使比值一示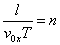 为一整数,则可以在电子射线管的荧光屏上观察到一个细小的亮点,这和一束近轴光线经过透镜后聚焦的现象类似,叫做磁聚焦。电子的纵向速度 为一整数,则可以在电子射线管的荧光屏上观察到一个细小的亮点,这和一束近轴光线经过透镜后聚焦的现象类似,叫做磁聚焦。电子的纵向速度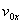 、可以由电子枪的加速电压 、可以由电子枪的加速电压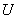 求得, 求得,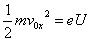 ,由式(8-69) ,由式(8-69)
(2)回旋加速器
回旋器是利用带电粒子在电场和磁场的联合作用下,用多次加速的方法来获得高能粒子的装置,它是原子核物理、高能物理等实验研究的一种基本设备。图8-28是回旋加速器的结构示意图,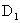 和 和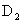 是封在高度真空室中的两个半圆形铜盒,常称为 是封在高度真空室中的两个半圆形铜盒,常称为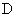 形电极。两个 形电极。两个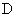 形电极与高频振荡器连接,于是在电极之间的缝隙处,就产生按一定频率变化着的交变电场。 形电极与高频振荡器连接,于是在电极之间的缝隙处,就产生按一定频率变化着的交变电场。
把两个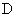 形电极放在电磁铁的两个磁极之间,便有一恒定的均匀强磁场垂直于电极板平面。如果在两盒间缝隙中央的 形电极放在电磁铁的两个磁极之间,便有一恒定的均匀强磁场垂直于电极板平面。如果在两盒间缝隙中央的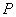 处由离子源发射出带电粒子,这些粒子在电场作用下被加速而进人盒 处由离子源发射出带电粒子,这些粒子在电场作用下被加速而进人盒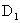 。当粒子在盒内运动时,因为盒内空间没有电场,粒子的速率将保持不变,但由于受到垂直方向恒定磁场的作用而作圆形轨道运动,根据式(8-68)其轨道半径 。当粒子在盒内运动时,因为盒内空间没有电场,粒子的速率将保持不变,但由于受到垂直方向恒定磁场的作用而作圆形轨道运动,根据式(8-68)其轨道半径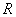 为 为
式中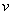 是粒子进人盒内的速率, 是粒子进人盒内的速率,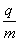 是粒子的比荷, 是粒子的比荷,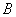 是磁感应强度。粒子在这一半盒内运动所需的时间 是磁感应强度。粒子在这一半盒内运动所需的时间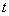 是 是
由上式可见, 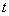 的大小仅与粒子的荷质比和磁感应强度有关。当粒子运动速度远小于光速时, 的大小仅与粒子的荷质比和磁感应强度有关。当粒子运动速度远小于光速时,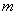 随速度的改变可以忽略不计,因此 随速度的改变可以忽略不计,因此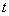 是常量,它与粒子的速度和粒子的回旋半径无关。如果振荡器的频率 是常量,它与粒子的速度和粒子的回旋半径无关。如果振荡器的频率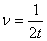 ,那么当粒子从 ,那么当粒子从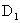 ,盒出来到达缝隙时,缝隙中的电场方向恰已反向,因而粒子将再被加速,以较大的速度进人 ,盒出来到达缝隙时,缝隙中的电场方向恰已反向,因而粒子将再被加速,以较大的速度进人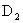 盒,并 盒,并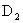 盒内以相应的较大半径作圆弧运动,再经过相同的时间 盒内以相应的较大半径作圆弧运动,再经过相同的时间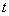 后,又回到缝隙而再次被加速进人 后,又回到缝隙而再次被加速进人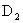 盒。所以,只要加在 盒。所以,只要加在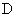 形电极上的高频振荡器的频率和粒子在 形电极上的高频振荡器的频率和粒子在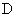 形盒中的旋转频率保持相等,便能保证带电粒子经过缝隙时受到电场力的加速。这样,随着加速次数的增加,轨道半径也将逐渐增大,形成图中所示螺液形线的运动轨道。最后将粒子用致偏电极 形盒中的旋转频率保持相等,便能保证带电粒子经过缝隙时受到电场力的加速。这样,随着加速次数的增加,轨道半径也将逐渐增大,形成图中所示螺液形线的运动轨道。最后将粒子用致偏电极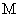 引出,从而获得高能粒子束,以进行实验工作。如果在粒子被引出前最后一圈的半径为 引出,从而获得高能粒子束,以进行实验工作。如果在粒子被引出前最后一圈的半径为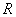 ,则引出粒子的速度为 ,则引出粒子的速度为
而粒子的动能是
上式表明,一个已建成的回旋加速器,它的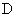 形电极的半径和最大磁感应强度都已确定,那么它能产生的最大能量的粒子也就确定了。 形电极的半径和最大磁感应强度都已确定,那么它能产生的最大能量的粒子也就确定了。
(3)质谱仪
带电粒子的电荷和质量是粒子的最基本的属性。对带电粒子的电荷量、质量和两者的比值的测定,在近代物理学的发展中是具有重大意义的,它是研究物质结构的基础。质谱仪是用磁场和电场的各种组合来达到把电荷量相等但质量不同的粒子分离开来的一种仪器,它是研究同位素的重要工具,也是测定离子比荷的仪器。
用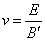 代入有 代入有
式中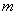 为离子的质量。如果离子是一价的, 为离子的质量。如果离子是一价的, 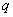 与电子的电荷量 与电子的电荷量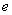 等值;如果是二价的, 等值;如果是二价的, 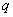 为 为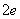 ,余类推。上式中 ,余类推。上式中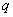 、 、 、 、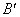 和 和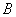 均为定值,因而 均为定值,因而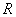 与离子质量 与离子质量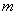 成正比,即从狭缝 成正比,即从狭缝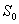 射出来的不同质量的同位素离子,在磁场 射出来的不同质量的同位素离子,在磁场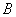 中作半径不同的圆周运动。因此,这些离子就将按照质量的不同而分别射到照相底片 中作半径不同的圆周运动。因此,这些离子就将按照质量的不同而分别射到照相底片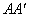 上的不同位置,形成若干线谱状的细条,每一细条相当于一定的质量。根据细条的位置可知圆周的半径R,因此可算出相应的质量,所以这种仪器叫做质谱仪。利用质谱仪可以精确地测定同位素的相对原子质量,图8-30是用质谱仪测得的锗( 上的不同位置,形成若干线谱状的细条,每一细条相当于一定的质量。根据细条的位置可知圆周的半径R,因此可算出相应的质量,所以这种仪器叫做质谱仪。利用质谱仪可以精确地测定同位素的相对原子质量,图8-30是用质谱仪测得的锗(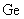 )元素的质谱,数字表示各同位素的相对质量数,即最靠近相对原子质量的整数。 )元素的质谱,数字表示各同位素的相对质量数,即最靠近相对原子质量的整数。
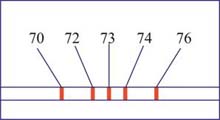
图 8-30 |
|
(4)霍耳(E.C.Hall)效应
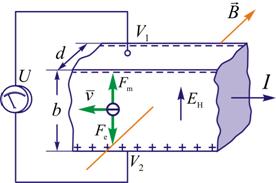
1879年霍耳首先观察到,把一载流导体薄板放在磁场中时,如果磁场方向垂直于薄板平面,则在薄板的上、下两侧面之间会出现微弱电势差(图8-31)。这一现象称为霍耳效应。这电势差称为霍耳电势差。
(a) |
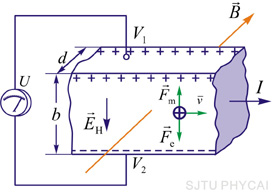
(b) |
图 8-31 |
实验测定,霍耳电势差的大小与电流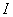 及磁感应强度 及磁感应强度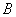 成正比,而与薄片沿 成正比,而与薄片沿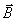 方向的厚度 方向的厚度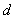 成反比,即 成反比,即
或写成
式中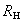 是一常量,称为霍耳系数,它仅与导体的材料有关。 是一常量,称为霍耳系数,它仅与导体的材料有关。
霍耳效应的出现是由于导体中的载流子(形成电流的运动电荷)在磁场中受洛伦兹力的作用而发生横向漂移的结果,以金属导体为例,导体中的电流是自由电子在电场作用下作定向运动形成的,其运动方向与电流的流向正好相反,如果在垂直电流方向有一均匀磁场B,这些自由电子受洛伦兹力作用,其大小为
式中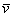 是电子定向运动的平均速度, 是电子定向运动的平均速度, 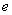 是电子电荷量的绝对值,力的方向向上。这时自由电子除宏观的定向运动外,还将向上漂移,这使得在金属薄板的上侧有多余的负电荷积累,而下侧缺少自由电子有多余的正电荷的积累,结果在导体内部形成方向向上的附加电场 是电子电荷量的绝对值,力的方向向上。这时自由电子除宏观的定向运动外,还将向上漂移,这使得在金属薄板的上侧有多余的负电荷积累,而下侧缺少自由电子有多余的正电荷的积累,结果在导体内部形成方向向上的附加电场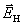 ,称为霍耳电场。这电场给自由电子的作用力 ,称为霍耳电场。这电场给自由电子的作用力
方向向下。当这两个力达到平衡时,电子不再有横向漂移运动,结果在金属薄板上下两侧间形成一恒定的电势差,由于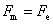 ,所以 ,所以
或
这样霍耳电势差
设单位体积内的自由电子数为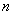 ,则电流 ,则电流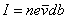 ,代人得 ,代人得
如果导侧中的载流子带正电荷量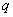 ,则洛伦兹力向上,使带正电的载流子向上漂移,这时霍耳电势差为 ,则洛伦兹力向上,使带正电的载流子向上漂移,这时霍耳电势差为
比较以上各式,可以得到霍耳系数
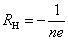 或 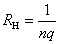 |
(8-90) |
霍耳系数的正负决定于载流子的正负性质。因此,实验侧定霍耳电势差或霍耳系数,不仅可以判定载流子的正负,还可以侧定载流子的浓度,即单位体积中的载流子数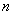 。例如,半导体材料就是用这个方法判定它是空穴型的( 。例如,半导体材料就是用这个方法判定它是空穴型的(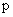 型—载流子为带正电的空穴)还是电子型的( 型—载流子为带正电的空穴)还是电子型的(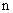 型—载流予是带负电的自由电子)。 型—载流予是带负电的自由电子)。
|






