例题10-1-1 如果水平光滑桌面上放着质量为 和 和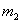 的二物块。它们之间被一根劲度系数为 的二物块。它们之间被一根劲度系数为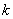 的轻弹簧连接着,试求该系统的振动周期。 的轻弹簧连接着,试求该系统的振动周期。
解:方法一:取如图1所示的坐标,设弹簧原长为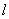 ,系统在振动过程中某时刻物块 ,系统在振动过程中某时刻物块 和 和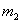 的坐标分别为 的坐标分别为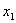 和 和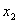 ,如图所示,分别对 ,如图所示,分别对 和 和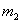 列出运动微分方程。 列出运动微分方程。
|
又 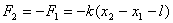 |
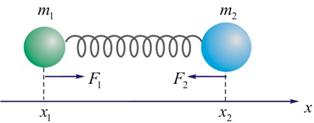
图1
|
(1)式(2)式分别改写成:
(4)式减(3)式:
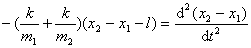
令 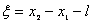 上式可改写为: 上式可改写为:
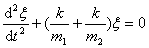
由此得该系统的谐振动周期: 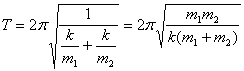
方法二:在质心坐标系解。我们先讨论一下弹簧的长度与劲度系数的关系,设弹簧原长为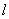 ,剪短以后的弹簧长为 ,剪短以后的弹簧长为 ,在相同力 ,在相同力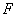 作用下,剪短后的弹簧 作用下,剪短后的弹簧 的伸长量为 的伸长量为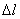 ,就要比原弹簧来得小。由弹簧的劲度系数定义: ,就要比原弹簧来得小。由弹簧的劲度系数定义:
原来弹簧的劲度系数: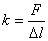
剪短后弹簧的劲度系数: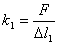
上二式相比得: 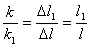
可知同一种弹簧它的劲度系数与它原长成反比。 |
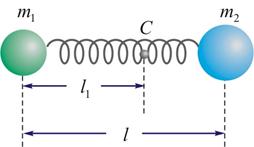
图2 |
由题意可知,弹簧对 和 和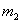 的作用力是系统的内力,系统在谐振动过程中质心 的作用力是系统的内力,系统在谐振动过程中质心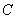 的位置相当于固定不动,作用于 的位置相当于固定不动,作用于 的弹簧长度 的弹簧长度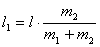 又根据上面讨论 又根据上面讨论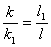
所以作用于 物块的弹簧劲度系数 物块的弹簧劲度系数
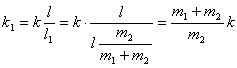
所以对于质量为 物块的弹簧振子的振动周期 物块的弹簧振子的振动周期
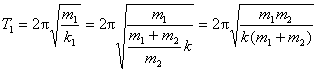
同理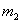 的弹簧振子周期 的弹簧振子周期 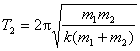
方法三:能量法解。
仍取如图1所示的坐标系,系统总机械能为:
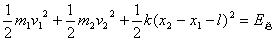
上式对时间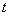 求导得: 求导得:
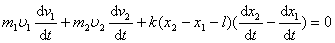
即
由于系统合外力等于零,系统动量守恒,因此
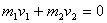 ,即 ,即 
将(5)式除以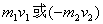 ,得: ,得:

即 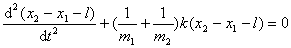
令 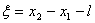 ,上式与方法一中的微分方程一样,同样得: ,上式与方法一中的微分方程一样,同样得:

|