1.受迫振动
摩擦阻尼总是客观存在的,只能减小而不能完全消除它。所以实际的振动物体如果没有能量的不断补充,振动最后总是要停止下来的。在实践中,为了获得稳定的振动,通常是对振动系统作用一周期性的外力。物体在周期性外力的持续作用下发生的振动称为受迫振动。这种周期性的外力称为驱动力。许多实际的振动属于受迫振动,例如,声波引起耳膜的振动、马达转动导致基座的振动等等。
为简单起见,假设驱动力有如下的形式:
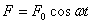
式中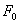 为驱动力的幅值, 为驱动力的幅值,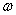 为驱动力的角频率。物体在弹性力、阻力和驱动力的作用下,其运动方程为: 为驱动力的角频率。物体在弹性力、阻力和驱动力的作用下,其运动方程为:
仍令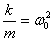 , ,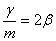 ,则上式可写成: ,则上式可写成:
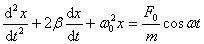
在阻尼较小的情况,上述方程的解为:
此解表示,在驱动力开始作用的阶段,系统的振动是非常复杂的[图10-8 (a)、(b)、(c)],可以看做是两个振动合成的,一个振动由式(10-21)中的第一项表示,它是一个减幅的振动;另一个振动由式(10-21)中的第二项表示,它是一个振幅不变的振动,经过一段时间之后,第一项分振动将减弱到可以忽略不计,余下的就是受迫振动达到稳定状态后的等幅振动,其振动表达式为
|
应该指出,稳态时的受迫振动的表式虽然和无阻尼自由振动的表式相同,都是简谐振动,但其实质已有所不同。首先,受迫振动的角频率不是振子的固有角频率,而是驱动力的角频率;其次,受迫振动的振幅和初相位不是决定于振子的初始状态,而是依赖于振子的性质、阻尼的大小和驱动力的特征。
从能量角度来看,在受迫振动中,振动物体因驱动力做功而获得能量(实际上在一个周期内驱动力有时做正功,有时做负功,但总效果还是做正功),同时又因阻尼作用而消耗能量。受迫振动开始时,驱动力所作的功往往大于阻尼消耗的能量,所以总的趋势是能量逐渐增大。由于阻尼力一般随速度哟增大而增大,当振动加强时,因阻尼而消耗的能量也要增多。在稳态振动的情况下,一个周期内,外力所作的功恰好补偿因阻尼而消耗的能量,因而系统维持等幅振动,如果撤去驱动力,振动能量又将逐渐减小而成为减幅振动。 |
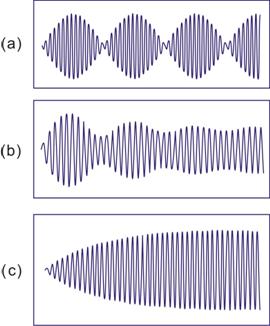
图 10-8 |
2.共振
对于一定的振动系统,如果驱动力的幅值一定,则受迫振动稳定态时的位移振幅随驱动力的频率而改变。按式(10-23)可以画出不同阻尼时位移振幅和外力频率之间的关系曲线(图10-9)。从图中可以看出,当驱动力的角频率为某个特定值时,位移振幅达到最大值,我们把这种位移振幅达到最大值的现象叫做位移共振,如果将式(10-23)对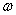 求导数,并 求导数,并
这表明,当驱动力的频率等于系统固有频率 时,速度幅值达到最大值。在给定幅值的周期性外力作用下,振动时的阻尼愈小,速度幅值的极大值也越大,共振曲线越为尖锐(图10-10)。 时,速度幅值达到最大值。在给定幅值的周期性外力作用下,振动时的阻尼愈小,速度幅值的极大值也越大,共振曲线越为尖锐(图10-10)。
由此可见,我们平常讲“驱动力的频率等于系统的固有频率时发生共振”,严格地说这是指速度共振,但是在阻尼很小的情况,速度共振和位移共振可以不加区分。
共振现象极为普遍,在声、光、无线电、原子物理及核物理以及工程技术领域中都会遇到。
反共振是指系统受迫振动时,如激励频率有微小的变化都会使系统响应增加的现象,这时称系统处于反共振状态。如果外加力的频率有任何微小的变化都会引起驱动点速度的增加,也就是频率恰使策动点的阻抗的绝对值为极大时,这时称为物体或系统与外加力发生速度反共振。如外加力的频率有任何微小的变化都会引起策动点的位移振幅增加,这时就称为物体或系统与外加力发生位移反共振。出现反共振现象的频率称为反共振频率。 |
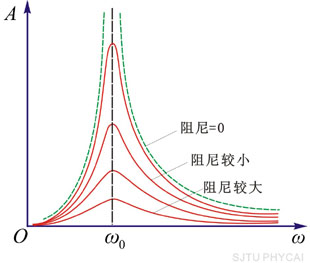
图 10-10 |
|