|
当一质点同时参与两个不同方向的振动时,质点的位移是这两个振动的位移的矢量和。在一般情形下,质点将在平面上作曲线运动。质点的轨道可有各种形状。轨道的形状由两个振动的周期、振幅和相位差来决定。
为简单起见,我们先讨论两个相互垂直的、同频率的简谐振动的合成。设两个简谐振动分别在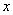 轴和 轴和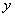 轴上进行,振动表式分别为: 轴上进行,振动表式分别为:
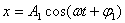
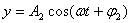
式中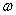 为两个振动的角频率, 为两个振动的角频率,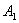 、 、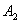 和 和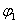 、 、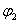 分别为两振动的振幅和初相位。在任一时刻 分别为两振动的振幅和初相位。在任一时刻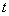 ,质点的位置是( ,质点的位置是(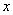 , ,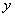 )。 )。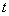 改变时,( 改变时,(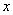 , ,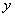 )也改变。所以上列两方程就是用参量 )也改变。所以上列两方程就是用参量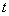 来表示质点运动轨道的参量方程.如果把参量 来表示质点运动轨道的参量方程.如果把参量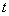 消去,就得到轨道的直角坐标方程: 消去,就得到轨道的直角坐标方程:
一般地说,上述方程是椭圆方程。因为质点的位移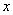 和 和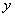 在有限范围内变动,所以椭圆轨道不会超出以 在有限范围内变动,所以椭圆轨道不会超出以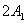 和 和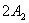 为边的矩形范围。按这两个振动在不同时刻的对应点,例如图10-16中两轴上的0、0;1、1;…等等,可以作出合运动的轨迹如图10-16所示。椭圆的性质(即长短轴的大小和方位),由相位差 为边的矩形范围。按这两个振动在不同时刻的对应点,例如图10-16中两轴上的0、0;1、1;…等等,可以作出合运动的轨迹如图10-16所示。椭圆的性质(即长短轴的大小和方位),由相位差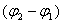 来决定。 来决定。
几种特殊情形
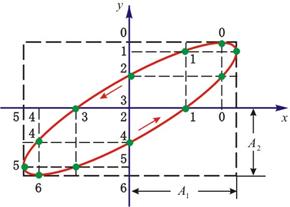
图 10-16 |
|
如果两个振动的频率相差很大,但有简单的整数比值的关系时,也可得到稳定的封闭的合成运动轨道。图10-17表示两个相互垂直、具有不同频率比(1:1、2:1、3:1和3:2)的简谐振动的合成的几个简单例子。两振动的频率为其他比值的类似曲线,种类很多,这里不一一绘出。这些曲线叫做李萨如(J.A. Lissajous)图形。利用这些图形,可由一已知频率求得另一个振动的未知频率;若频率比也已知,则可利用这种图形确定相位关系,这是无线电技术中常用的测定频率、确定相位关系的方法。
这里所讨论的振动合成还仅是一些特殊的情况。在一般情况下,也不难证明:一个复杂的直线振动总可以认为是沿同一直线的许多不同频率的简谐振动的合成。因此正如本章开始时所指出的,简谐振动的规律是研究复杂振动规律的基础。 |
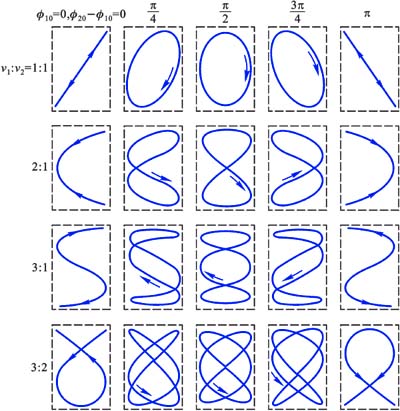 图 10-17
图 10-17 |
|