1.波函数
为了定量地描述波在空间的传播,需要用数学函数式来表示介质中各质点的振动状态随时间变化的关系。这样的关系式称为波动表达式,或称为波函数。一般写成
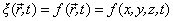
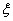 可以表示各种各样的物理量。例如质点的位移、弹性介质的形变、气体的压强等等,它反映了任一时刻振动着的物理量在空间的分布情况。 可以表示各种各样的物理量。例如质点的位移、弹性介质的形变、气体的压强等等,它反映了任一时刻振动着的物理量在空间的分布情况。
2.平面简谐波的波函数
平面简谐波(余弦波或正弦波)最为简单,也最为基本.我们先讨论平面余弦行波在理想的无吸收的均匀无限大介质中传播时的波函数。

若介质中的波速为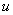 ,则 ,则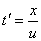 ,代人上式并将下角标 ,代人上式并将下角标 省去得到 省去得到
上式所表示的是波线上任一点(距原点为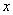 )处的质点任一瞬时的位移,这就是我们所需要的沿 )处的质点任一瞬时的位移,这就是我们所需要的沿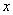 轴方向前进的平面简谐波的波函数。 轴方向前进的平面简谐波的波函数。
我们把单位长度上波的相位变化称为角波数,用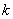 表示,它的数值等于 表示,它的数值等于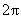 长度内所包含的完整波的个数,则 长度内所包含的完整波的个数,则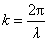 。 。
利用关系式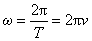 和 和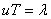 及 及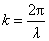 ,可以将平面简谐波的波函数改写成多种形式 ,可以将平面简谐波的波函数改写成多种形式
在导出上述平面余弦波的波函数时,我们假定波动是沿着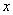 轴的正方向传播的,如果波动沿 轴的正方向传播的,如果波动沿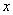 轴的负方向传播,则 轴的负方向传播,则
应该注意区别波形的传播速度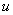 和介质中质点的振动速度 和介质中质点的振动速度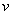 。 。 |