1.波的能量
当机械波传播到介质中的某处时,该处原来不动的质点开始振动,因而具有动能,同时该处的介质也将产生形变,因而也具有势能。波动传播时,介质由近及远地振动着,由此可见,能量是向外传播出去的。这是波动的重要特征。
下面我们仅以平面余弦弹性纵波在棒中传播的特殊情况为例,对能量的传播作简单说明。
在棒中任取体积为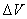 、质量为 、质量为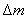 ( (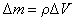 , ,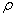 为棒的体密度)的体积元。当波动传播到这个体积元时,这体积元将具有动能 为棒的体密度)的体积元。当波动传播到这个体积元时,这体积元将具有动能 和弹性势能 和弹性势能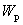 。如果棒中平面简谐波的表达式为 。如果棒中平面简谐波的表达式为
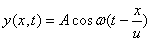
可以证明
而体积元的总机械能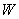 为 为
总能量是时间的函数。这表明波动传播能量。
介质中单位体积的波动能量,称为波的能量密度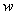 ,即 ,即
波的能量密度是随时间而变化的,通常取其在一个周期内的平均值。因为正弦函数的平方在一个周期内的平均值为1/2,所以能量密度在一个周期内的平均值为
这一公式虽然是从平面余弦弹性纵波的特殊情况导出的,但是机械被的能量与振幅的平方、频率的平方都成正比的结论却是对于所有弹性波都是适用的。
2.波的强度
根据以上分析,能量是随着波动的进行在介质中传播的,所以我们可以引人能流的概念。
单位时间内通过介质中某面积的能量称为通过该面积的能流。设在介质中垂直于波速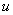 取面积 取面积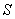 ,则在单位时间内通过 ,则在单位时间内通过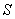 面的能量等于体积 面的能量等于体积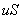 中的能量(图11-9)这能量是周期性变化的,通常取其一个周期的时间平均值,即得平均能流为 中的能量(图11-9)这能量是周期性变化的,通常取其一个周期的时间平均值,即得平均能流为
式中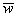 是平均能量密度。 是平均能量密度。
通过与波动传播方向垂直的单位面积的平均能流,称为平均能流密度或波的强度,用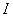 来表示,即 来表示,即 |
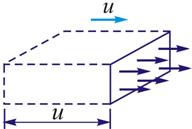
图11-9 |
其中
是表征介质特性的一个常量,称为介质的特性阻抗。式(11-21)表明,弹性介质中简谐波的强度正比于振幅的二次方,正比于角频率(或频率)的二次方,还正比于介质的特性阻抗。在国际单位制中,波的强度的单位为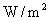 。 。
平面波和球面波的振幅
3.波的吸收
实际上,平面行波在均匀介质中传播时,介质总是要吸收波的一部分能量,因此波的强度和振幅都将逐渐减小。所吸收的波动能量将转化成其他形式的能量(例如介质的内能)。这种现象称为波的吸收。有吸收时,平面波振幅的衰减规律可用下法求出:通过极薄的(厚度为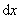 )一层介质后,振幅的减弱( )一层介质后,振幅的减弱(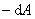 )应该正比于此处的振幅 )应该正比于此处的振幅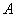 ,也正比于这厚度 ,也正比于这厚度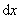 ,即 ,即
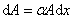
经过积分,便得
式中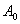 和 和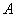 分别为 分别为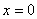 和 和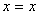 处的振幅, 处的振幅,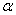 为决定于介质并与频率有关的常数,称为介质的吸收系数, 为决定于介质并与频率有关的常数,称为介质的吸收系数,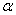 的值不仅取决于介质种类,而且与波的频率 的值不仅取决于介质种类,而且与波的频率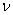 有关,情况相当复杂。从大体上说,流体的吸收系数正比于 有关,情况相当复杂。从大体上说,流体的吸收系数正比于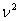 ,而固体的吸收系数正比于 ,而固体的吸收系数正比于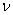 。 。
由于波的强度与振幅的平方成正比,所以平面波强度衰减的规律是
式中的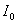 和 和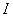 分别为 分别为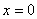 和 和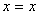 处的波的强度。 处的波的强度。
|