1.惠更斯原理
波动的起源是波源的振动,波的传播是由于介质中质点之间的相互作用。介质中任一点的振动将引起邻近质点的振动,因而在波的传播过程中,介质中任何一点都可以看做新的波源。
惠更斯总结了上述现象,提出了关于波的传播规律:在波的传播过程中,波阵面(波前)上的每一点都可看做是发射子波的波源,在其后的任一时刻,这些子波的包迹就成为新的波阵面。这就是惠更斯原理。 |
应该指出,惠更斯原理并没有说明各个子波在传播中对某一点的振动究竟有多少贡献。我们将在本篇波动光学部分介绍菲涅耳对惠更斯原理所作的补充。
2.波的衍射
当波在传播过程中遇到障碍物时,其传播方向绕过障碍物发生偏折的现象,称为波的衍射(旧称绕射)。如图11-17所示,平面波通过一狭缝后能传到按直线前进所形成的阴影区域内。这一现象可用惠更斯原理作出解释。当波阵面到达狭缝时,缝处各点成为子波源,它们发射的子波的包迹在边缘处不再是平面,从而使传播方向偏离原方向而向外延展,进入缝两侧的阴影区域。图11-18为水波通过小屏障和小孔的衍射图样。
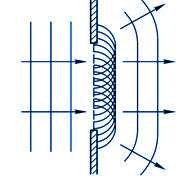
图11-17 |
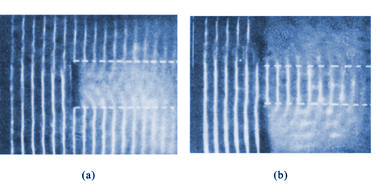
图11-18 |
3.波的反射和折射
波动从一种介质传到另一种介质时,在两种介质的分界面上,传播方向要发生变化,产生反射和折射现象。根据实验的结果,可得到波动的反射定律和折射定律。下面用惠更斯原理来推导这些定律。
反射定律:入射线、反射线和分界面的法线均在同一平面内;入射角等于反射角。
折射定律:不论入射角大小如何,入射角的正弦与折射角的正弦之比都等于波在第一介质中的波速与第二介质中的波速之比。即
用惠更斯原理也可推导出这些定律。
4.反射波、透射波的强度和相位
反射波、透射波的振幅与入射波的振幅之比可写成
由此可以知道,如果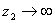 或 或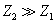 ,这种极端情况相当于介质2是一种刚性壁,例如绳子的一端固定在墙上,由于墙的特性阻抗 ,这种极端情况相当于介质2是一种刚性壁,例如绳子的一端固定在墙上,由于墙的特性阻抗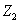 比绳子的特性阻抗 比绳子的特性阻抗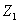 大得多,这种情况对绳来说也称“固定端”情况。这时在界面上反射波的波动与入射波的振动始终反相位。如反射波的振幅与入射波的振幅相等,则在固定端的合振动恒为零。如果 大得多,这种情况对绳来说也称“固定端”情况。这时在界面上反射波的波动与入射波的振动始终反相位。如反射波的振幅与入射波的振幅相等,则在固定端的合振动恒为零。如果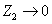 或 或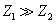 ,这又是一种极端情况。例如棒时一端固定,另一端置于空气中,由于空气的特性阻抗 ,这又是一种极端情况。例如棒时一端固定,另一端置于空气中,由于空气的特性阻抗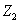 相对于棒的特性阻抗 相对于棒的特性阻抗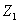 ,可以略去,这种情况对棒来说也称“自由端”情况。这时在界面上反射波的振动与入射波振动相位完全相同,在自由端的合振幅恒为极大。 ,可以略去,这种情况对棒来说也称“自由端”情况。这时在界面上反射波的振动与入射波振动相位完全相同,在自由端的合振幅恒为极大。
5.电磁波的反射和折射
设有平面电磁波从一介质(折射率为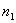 )以入射角 )以入射角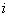 射向另一介质(折射率为 射向另一介质(折射率为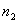 ),在界面上将发生反射和透射现象,其反射角为 ),在界面上将发生反射和透射现象,其反射角为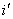 (= (=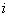 ),折射角为 ),折射角为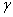 。我们将入射电磁波的电场矢量 。我们将入射电磁波的电场矢量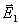 分解为垂直于入射面的分矢量 分解为垂直于入射面的分矢量 和平行于入射面的分矢量 和平行于入射面的分矢量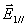 (相应地,磁场矢量 (相应地,磁场矢量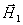 也分解为 也分解为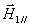 和 和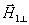 两个分矢量),它们的方向如图11-20a所示,反射波和折射波的电场矢量 两个分矢量),它们的方向如图11-20a所示,反射波和折射波的电场矢量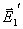 和 和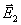 也可分解为平行于入射面的分矢量 也可分解为平行于入射面的分矢量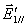 、 、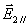 和垂直于入射面的分矢量 和垂直于入射面的分矢量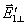 、 、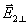 。注意图中所画的各分矢量方向分别表示各量所取的正方向,而不是入射波、反射波和折射波电场矢量的实际方向,如计算结果为正值,则该分矢量与图中所示方向一致,反之,则与图中所示方向相反。我们可用和机械波类似的处理方法,并利用电磁场的边界条件,可以导出如下关系式: 。注意图中所画的各分矢量方向分别表示各量所取的正方向,而不是入射波、反射波和折射波电场矢量的实际方向,如计算结果为正值,则该分矢量与图中所示方向一致,反之,则与图中所示方向相反。我们可用和机械波类似的处理方法,并利用电磁场的边界条件,可以导出如下关系式:
|
(11-51) |
|
(11-52) |
|
(11-53) |
|
(11-54) |
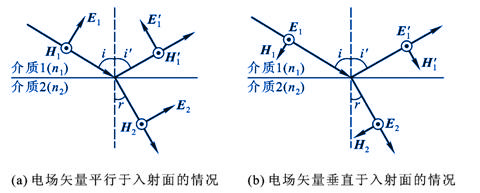
图11-20 |
以上四式就是著名的菲涅耳反射折射公式。其中式(11-51)和式(11-53)是反射公式,式(11-52)和式(11-54)是折射公式。反射波的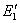 和入射波的 和入射波的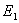 之比(对垂直分量是 之比(对垂直分量是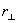 ,平行分量是 ,平行分量是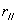 )称为振幅反射系数,透射波的 )称为振幅反射系数,透射波的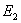 和入射波的 和入射波的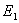 之比( 之比(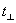 和 和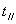 )称为振幅透射系数。它们的平方分别称为强度反射系数和强度透射系数。菲涅耳公式是研究波动光学的基础,可以确定反射光的相位和强度以及偏振程度等。 )称为振幅透射系数。它们的平方分别称为强度反射系数和强度透射系数。菲涅耳公式是研究波动光学的基础,可以确定反射光的相位和强度以及偏振程度等。
当电磁波垂直入射时,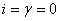 ,根据反射系统定义得振幅反射系数 ,根据反射系统定义得振幅反射系数
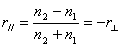
强度反射系数
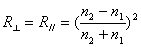
以玻璃为例,设其折射率为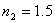 ,光从空气( ,光从空气(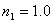 )垂直入射在玻瑞表面时 )垂直入射在玻瑞表面时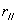 = 20%, = 20%,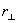 =-20%, =-20%,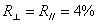 。这就是说,入射光中的光能,有4%的能量反射回空气,有96%的能量透射入玻璃。 。这就是说,入射光中的光能,有4%的能量反射回空气,有96%的能量透射入玻璃。 |