1.机械波的多普勒效应
我们前面所讨论的波源(或说接收器),相对于介质都是静止的。但是在日常生活和科学观测中,经常会遇到波源或观察者相对于介质而运动的情况。例如,火车汽笛的音调,在接近观察者时比其远离时为高。这种因波源或视察者相对于介质的运动,而使观察者接收到的波的频率有所变化的现象是由多普勒(J.C.Doppler)在1842年首先发现的,故称为多普勒效应。下面就来分析这一现象。
为简单起见,我们假定波源、观察者的运动发生在二者的连线上,设波源相对于介质的运动速度为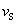 ,观察者相对于介质的运动速度为 ,观察者相对于介质的运动速度为 ,以 ,以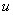 表示波在介质中传播的速度。波源的频率、观察者接收到的频率和波的频率分别用 表示波在介质中传播的速度。波源的频率、观察者接收到的频率和波的频率分别用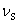 、 、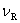 、 、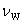 表示。只有当波源和观察者相对介质静止时,三者是相等的。现在分别讨论三种情况。 表示。只有当波源和观察者相对介质静止时,三者是相等的。现在分别讨论三种情况。
(1)波源不动,观察者以速度 相对于介质运动。 相对于介质运动。
由于波源在介质中静止,所以波的频率就等于波源的频率,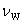 = =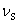 ,因而有 ,因而有
所以观察者向波源运动时所接收到的频率为波源频率的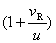 倍。 倍。
当观察者远离波源运动时,按类似的分析,可得观察者接收到的频率为
即此时接收到的频率低于波源的频率。综合(11-64)、(11-65)两式,只要将 理解为代数值,并且规定,观察者接近波源时 理解为代数值,并且规定,观察者接近波源时 为正值;远离波源时为负值,则当波源不动,现察者以 为正值;远离波源时为负值,则当波源不动,现察者以 相对波源运动时所接收到的频率可统一表示为 相对波源运动时所接收到的频率可统一表示为
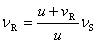
(2)观察者不动,波源以速度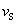 相对于介质运动。 相对于介质运动。
波源在运动中仍按自己的频率发射波,在一个周期 内,波在介反中传播了距离 内,波在介反中传播了距离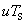 ,完成了一个完整的波形。设波源向着观察者运动。在这段时间内,波源位置由 ,完成了一个完整的波形。设波源向着观察者运动。在这段时间内,波源位置由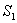 移到 移到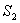 ,移过距离 ,移过距离 (图11-27a)。由于波源的运动,介质中的波长变小了,实际波长为 (图11-27a)。由于波源的运动,介质中的波长变小了,实际波长为

图11-27 |
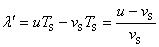
相应地,波的频率为
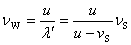
由于观察者静止,所以他接收到的频率就是波的频率,即
此时观察者接收到的频率大于波源的频率。
当波源远离观察者运动时,介质中的实际波长
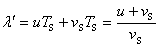
按类似的分析,可得观察者接收到的频率为
这时观察者接收到的频率低于波源的频率。
同样地,如果将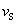 理解为代数值,并规定波源接近接收器时为正值,远离接收器时为负值,则(11-66)、(11-67)两式可统一表示为 理解为代数值,并规定波源接近接收器时为正值,远离接收器时为负值,则(11-66)、(11-67)两式可统一表示为
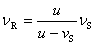 |
(11-68) |
图11-27(b)表示波源在移动时每个波动造成的波阵面,其球面不是同心的。从图上可以清楚地看出,在波源运动的前方波长变短,后方波长变长。
(3)观察者与波源同时相对介质而运动。
根据以上的讨论,由于波源的运动,介质中波的频率为
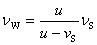
由于观察者的运动,观察者接收到的频率与波的频率之间的关系为
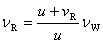
代入上式得观察者接收到的频率为
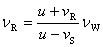
当波源和观察者相向运动时,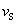 和 和 均取正值;当波源和观察者相背运动时, 均取正值;当波源和观察者相背运动时,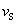 和 和 均为负值。 均为负值。
如果波源和观察者是沿着它们的垂直方向运动,则不难推知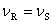 , 即没有多普勒效应发生。又如果波源和观察者的运动是任意方向的,那么只要将速度在连线上的分量代入上述公式即可。不过随着两者的运动,在不同时刻 , 即没有多普勒效应发生。又如果波源和观察者的运动是任意方向的,那么只要将速度在连线上的分量代入上述公式即可。不过随着两者的运动,在不同时刻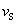 和 和 的分量也不同,这种情况下接收到的频率将随着时间变化。 的分量也不同,这种情况下接收到的频率将随着时间变化。
2.电磁波的多普勒效应
多普勒效应是波动过程的共同特征。不仅机械波有多普勒效应,电磁波(包括光波)也有多普勒效应。因为电磁波的传播不依赖弹性介质,所以波源和观测者之间的相对运动速度决定了接收到的频率。电磁波以光速传播,在涉及相对运动时必须考虑相对论时空变换关系。计算证明,当波源和观测者在同一直线上运动时
式中 表示波源和接收器之间相对运动的速度,当波源与观测者相互接近时, 表示波源和接收器之间相对运动的速度,当波源与观测者相互接近时, 取正值;当波源与观测者相互远离时, 取正值;当波源与观测者相互远离时, 取负值。前者接收到的频率比发射频率高,称为紫移;后者接收到的频率比发射频率低,称为红移。 取负值。前者接收到的频率比发射频率高,称为紫移;后者接收到的频率比发射频率低,称为红移。
电磁波和光的多普勒效应有着广泛的应用。
3.冲击波
当波源运动的速度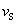 超过波的速度 超过波的速度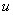 时,式(11-67)的计算结果( 时,式(11-67)的计算结果(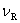 <0)将没有意义。这时波源将位于波前的前方。如图11-28所示。当波源在 <0)将没有意义。这时波源将位于波前的前方。如图11-28所示。当波源在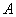 位置时发出的波,在其后 位置时发出的波,在其后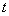 时刻的波阵面为半径等于 时刻的波阵面为半径等于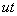 的球面,但此时刻波源已前进了 的球面,但此时刻波源已前进了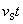 的距离到达 的距离到达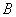 位置,在整个 位置,在整个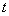 时间内,波源发出的波的各波前的切面形成一个圆锥面,这锥形的顶角满足 时间内,波源发出的波的各波前的切面形成一个圆锥面,这锥形的顶角满足
|
随看时间的推移,各波前不断扩展,锥面也不断扩展,这种以点波源为顶点的圆锥形的波称为冲击波。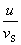 通常称为马赫数, 通常称为马赫数,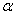 称为马赫角。锥面就是受扰动的介质与未受扰动的介质的分界面,在两侧有着压强、密度和温度的突变。 称为马赫角。锥面就是受扰动的介质与未受扰动的介质的分界面,在两侧有着压强、密度和温度的突变。
|
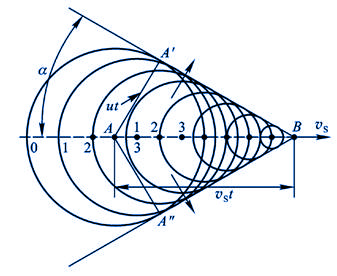
图11-28 |
|