处于激发态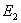 的原子,在频率为 的原子,在频率为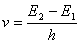 的外界光子的激励下,跃迁到低能级 的外界光子的激励下,跃迁到低能级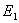 上去,同时发出一个与外来光子完全相同的光子,这种过程称为受激辐射,如图14-3所示。 上去,同时发出一个与外来光子完全相同的光子,这种过程称为受激辐射,如图14-3所示。
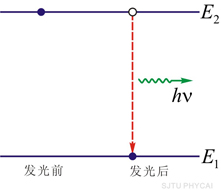
图14-3 受激辐射能级示意图 受激辐射发出的光子与外来光子具有完全相同的特征,即频率、相位、偏振状态和传播方向完全相同。所以,受激辐射的光是相干的。
设想有一个外来的光子入射,它会使处于激发态的某原子产生受激辐射,于是得到了两个特征完全相同的光子。在传播过程中,这两个光子再引起其他原子产生受激辐射,就能得到4个特征完全相同的光子……这样继续下去,只要传播路程足够长,在一个外来的入射光子作用下,就会引起大量原子产生受激辐射,产生大量特征完全相同的光子,这个现象称为光放大。
设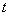 时刻处于激发态 时刻处于激发态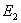 上的原子数为 上的原子数为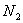 , ,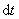 时间内由于受激辐射从 时间内由于受激辐射从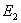 跃迁到低能级 跃迁到低能级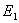 上的原子数为 上的原子数为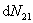 ,频率 ,频率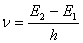 的入射光的辐射能密度为 的入射光的辐射能密度为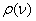 ,则三者间有下述关系: ,则三者间有下述关系:
式中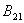 为爱因斯坦受激辐射系数。 为爱因斯坦受激辐射系数。
爱因斯坦系数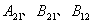 之间满足某种关系,即爱因斯坦关系,可如下求得:光和原子体系相互作用时,受激辐射、受激吸收、自发辐射总是同时存在的。当处于热平衡状态时, 之间满足某种关系,即爱因斯坦关系,可如下求得:光和原子体系相互作用时,受激辐射、受激吸收、自发辐射总是同时存在的。当处于热平衡状态时,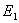 和 和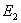 能级上的原子数达到稳定分布,入射光的能量密度 能级上的原子数达到稳定分布,入射光的能量密度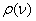 也保持为常数(黑体辐射)。则 也保持为常数(黑体辐射)。则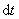 时间内由于受激吸收从能级 时间内由于受激吸收从能级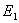 跃迁到能级 跃迁到能级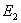 上的原子数 上的原子数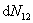 应等于由于受激辐射和自发辐射而从能级 应等于由于受激辐射和自发辐射而从能级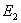 跃迁到能级 跃迁到能级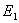 上的原子数,即 上的原子数,即
由上式可得
把式(14-3)代入式(14-8),并考虑到 ,得
把普朗克黑体辐射公式 ,得
把普朗克黑体辐射公式
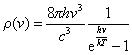
与式(14-9)比较,即可得到爱因斯坦关系
|