(1)零电阻 零电阻是超导体的一个重要特性。超导体处于超导态时电阻完全消失。若用它组成闭合回路,一旦在回路中有电流,则回路中没有电能的消耗,不需要任何电源补充能量,电流可以持续存在下去,形成所谓持久电流。柯林斯(J. Collins)曾将一铅环放在垂直于环面的磁场中,将其冷却到超导的转变温度以下,然后撤去磁场,这时在环中产生感应电流。他观察电流的衰减情况,结果在长达两年半时间内也未观测到电流有丝毫的衰减。所以,超导体是具有理想导电性的导体。
(2)临界磁场与临界电流 1913年,昂内斯曾企图用超导铅线绕制超导磁体。但他发现,当超导铅线中的电流超过某一临界值时,铅线就转变为正常态。1914年,他从实验中发现,材料的超导态可以被外加磁场破坏而转入正常态。这种破坏超导态所需的最小磁场强度称为临界磁场,以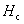 表示。临界磁场与材料的种类和超导态所处的温度有关,一般说来,临界磁场与温度有如下关系 表示。临界磁场与材料的种类和超导态所处的温度有关,一般说来,临界磁场与温度有如下关系
如图15-20所示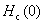 表示 表示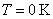 时的临界磁场。不同材料的 时的临界磁场。不同材料的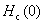 不同,如表15-2所示。 不同,如表15-2所示。
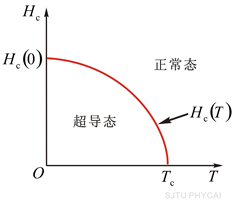
图15-20 临界磁场与温度的关系
临界磁场的存在,限制了超导体中能够通过的电流。当通过超导体导线的电流超过一定数值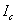 后,超导态便被破坏, 后,超导态便被破坏,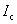 称为超导体临界电流,这是因为当超导体通上电流以后,这电流也将产生磁场,当该电流在超导体表面所产生的磁场强度等于 称为超导体临界电流,这是因为当超导体通上电流以后,这电流也将产生磁场,当该电流在超导体表面所产生的磁场强度等于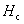 时,电流自身产生的磁场破坏了超导态,临界电流与温度的关系如下: 时,电流自身产生的磁场破坏了超导态,临界电流与温度的关系如下:
式中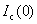 表示 表示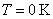 时超导体的临界电流。 时超导体的临界电流。
综上所述,可以得出超导态的三个临界条件:临界温度、临界磁场和临界电流,它们之间密切相关。
大多数纯金属超导体的磁场与温度关系如图15-20所示。若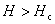 时,它由超导态直接转变为正常态,这种超导体称为第 时,它由超导态直接转变为正常态,这种超导体称为第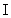 类超导体。还有一类超导体,在低于临界温度的一定温度下,有两个临界磁场 类超导体。还有一类超导体,在低于临界温度的一定温度下,有两个临界磁场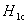 和 和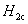 ,如图15-21所示。当材料处在磁场 ,如图15-21所示。当材料处在磁场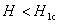 下时,为纯粹超导态,或称迈斯纳态;当磁场增强至 下时,为纯粹超导态,或称迈斯纳态;当磁场增强至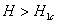 时,它们不是从超导态直接转变为正常态,面是超导态和正常态混杂的混合态,直到磁场 时,它们不是从超导态直接转变为正常态,面是超导态和正常态混杂的混合态,直到磁场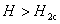 时才完全转变为正常态。这类超导体称为第 时才完全转变为正常态。这类超导体称为第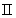 类超导林。如铌、钒和一些合金和化合物材料。第 类超导林。如铌、钒和一些合金和化合物材料。第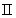 类超导体的 类超导体的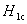 一般不超过 一般不超过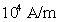 ,但 ,但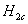 很高,约为 很高,约为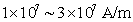 。例如,银三锡 。例如,银三锡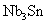 的 的 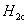 在 在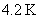 时可达 时可达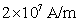 ,而在这样高的磁场下,第 ,而在这样高的磁场下,第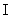 类超导体早已失去了超导性,正是由于第 类超导体早已失去了超导性,正是由于第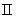 类超导体具有很高的 类超导体具有很高的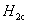 ,因而有重要的实用价值。 。 ,因而有重要的实用价值。 。
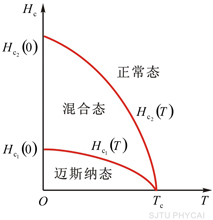
图15-21 第 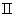 类超导体的临界磁场与温度的关系 |

图15-22 第 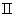 类超导体的混合态结构 |
当第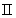 类超导体处于混合态时,其结构如图15-22所示。整个材料是超导的,在材料内部出现许多沿外磁场方向、半径极小的圆柱形正常态区域,可称为正常芯。这些正常芯排列成一种周期性的规则图案,各正常芯的间距在 类超导体处于混合态时,其结构如图15-22所示。整个材料是超导的,在材料内部出现许多沿外磁场方向、半径极小的圆柱形正常态区域,可称为正常芯。这些正常芯排列成一种周期性的规则图案,各正常芯的间距在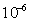 到 到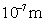 之间。每根正常芯表面上围绕着涡旋状电流,这些电流屏蔽了芯中的磁场对外面超导区的作用。因此正常芯好像是外磁场的通道。实验证明,在每条芯中的磁通量都相等,且有一个确定的值 之间。每根正常芯表面上围绕着涡旋状电流,这些电流屏蔽了芯中的磁场对外面超导区的作用。因此正常芯好像是外磁场的通道。实验证明,在每条芯中的磁通量都相等,且有一个确定的值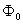 ,即 ,即
式中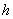 为普朗克常量, 为普朗克常量,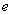 为电子的电荷量。这说明磁通量是量子化的, 为电子的电荷量。这说明磁通量是量子化的,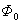 就是磁通量子。当外磁场增加时,不能增加每根正常芯内的磁通量,只能增加正常芯的数目。磁场越强,正常芯越多越密,一直到磁场增大到 就是磁通量子。当外磁场增加时,不能增加每根正常芯内的磁通量,只能增加正常芯的数目。磁场越强,正常芯越多越密,一直到磁场增大到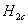 时,正常芯将充满整个材料而使材料全部转变为正常态。如果在垂直于外磁场方向的材料断面上撒上极细的铁粉(直径约 时,正常芯将充满整个材料而使材料全部转变为正常态。如果在垂直于外磁场方向的材料断面上撒上极细的铁粉(直径约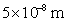 ),在电子显微镜下就能清楚地观察到正常芯作规则排列的图象。 ),在电子显微镜下就能清楚地观察到正常芯作规则排列的图象。
(3)迈斯纳效应–完全抗磁性 零电阻是超导体的一个基本特性,但超导体的完全抗磁性更为基本。因此,人们在探索新的超导体时,为判断发生的是否正常态向超导态转变,必须综合这两种测量结果,才能予以确定。
如果将一超导体样品放人磁场中,由于穿过样品的磁通量发生了变化,所以在样品表面产生电流,如图15-22所示,这电流将在样品内部产生磁场,完全抵消掉内部的外磁场,使超导体内部的磁场为零。根据公式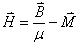 和 和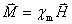 ,由于超导体内 ,由于超导体内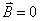 ,故 ,故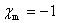 。所以超导体具有完全抗磁性。 。 。所以超导体具有完全抗磁性。 。
1933年,迈斯纳(W. F. Meissner )和奥赫森菲尔德(R. Ochsenfeld)进一步实验发现,如果把临界温度以上的超导体样品放入磁场中,由于这时样品不是处于超导态,故其中有磁场存在,当维持磁场不变而降低样品温度使其处于超导态时,其内部也没有磁场了,如图15-23所示。这是因为在转变过程中,在超导体表面上也产生电流,这电流在其内部的磁场完全抵消了原来的磁场,使超导体内磁感应强度为零。
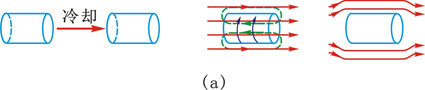
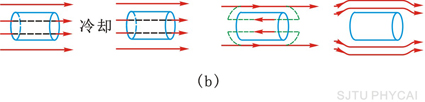
(a)先冷却后加磁场(b)先加磁场后冷却
图15-23 迈斯纳效应
总结上面的实验结果,得到结论是:在使样品转变为超导态的过程中,无论先降温后加磁场,还是先加磁场后降温,超导体内部的磁感应强度总是为零。这一现象称为迈斯纳效应。
超导体的完全抗磁性可以用实验演示,将一个涂有超导材料的小球放在铅直的外磁场中(图15-24),由于它的磁化方向与外磁场方向相反,它将受到一个向上的斥力,这斥力与重力平衡时,小球被悬浮在空中。当重力发生微小变化时,小球就会上下移动。若把小球位置上下变化的情况精确地记录下来,就可以精确地测定重力的微小变化。由此可以造成极灵敏的超导重力仪。
(4)同位素效应 为了探讨超导转变温度与物质成分的关系,对许多同位素进行试验。结果表明,同位素的质量数愈大,转变温度愈低。例如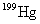 的 的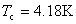 , , 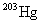 的 的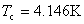 。1950年雷诺(C.A. Reynolds)和麦克斯韦(E. Maxwell)等分别得到如下规律 。1950年雷诺(C.A. Reynolds)和麦克斯韦(E. Maxwell)等分别得到如下规律
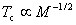
这称为同位素效应。我们知道,同一元素的不同同位素,所不同的地方在于原子核的质量,所以同位素效应表明在超导电现象中,电子和晶格的相互作用是一个重要的原因。
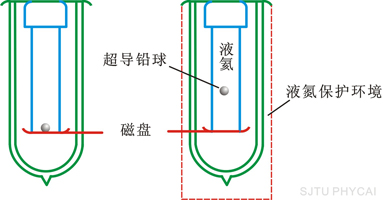
图15-24 磁悬浮
|
