|
人们发现的2000多种同位素可分为两大类:一类是稳定的,另一类是不稳定的。稳定核素是指其原子核不会自发地发生变化而变成其他原子。自然界存在的稳定核素约为270个。不稳定核素是指其原子核会自发地蜕变转变成另一种原子核会或另一种同位素,同时放出各种射线,这样的现象称为放射性衰变。
1896年贝可勒尔(H. Bacquerel )首先发现了铀的放射性现象,随后于1898年居里夫妇(P. &M.Curie)又发现了放射性元素钋和镭,这是人类认识原子核的开始。1934年约里奥·居里夫妇(F. &I.
Joliot-Curie)发现人工放射性,从而开始人工制备放射性元素,并为应用放射性开辟了广阔的途径。
迄今为止,人们已发现的放射性衰变模式主要有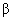 衰变、 衰变、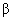 衰变和 衰变和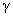 衰变( 衰变(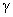 跃迁))。 跃迁))。
(1)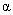 衰变 衰变
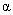 衰变是指不稳定核自发地放出带两个正电荷的氦核 衰变是指不稳定核自发地放出带两个正电荷的氦核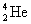 (又称 (又称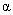 粒子)而发生转变的过程。例如 粒子)而发生转变的过程。例如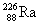 (镭)核的 (镭)核的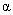 衰变过程如下 衰变过程如下
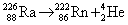
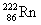 (氡)核也具有 (氡)核也具有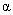 放射性 放射性
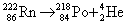
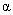 衰变使母核失去2个与电子电荷量相等的正电荷,因此衰变后原子序数减少2,而子核在周期表上的位置将向前移2位,质量数应减小4, 衰变使母核失去2个与电子电荷量相等的正电荷,因此衰变后原子序数减少2,而子核在周期表上的位置将向前移2位,质量数应减小4,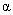 衰变一般表示为 衰变一般表示为
衰变前,母核X可以看做静止,根据能量守恒定律我们有
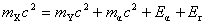
式中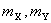 和 和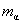 分别是母核、子核和粒子的静止质量; 分别是母核、子核和粒子的静止质量;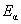 和 和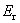 分别为粒子的动能和子核的反冲动能。 分别为粒子的动能和子核的反冲动能。
定义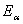 与 与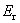 之和为“ 之和为“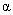 衰变能”并记作 衰变能”并记作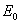 。因此 。因此
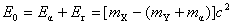
如果忽略电子与原子核之间的结合能,我们可用原子的质量代替原子核的质量。于是, 衰变能 衰变能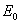 为 为
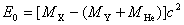
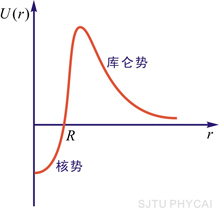
图16-10 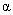 粒子受到的势垒 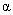 衰变的理论是量子力学最早应用于核物理并取得了成功的例子之一。在核内, 衰变的理论是量子力学最早应用于核物理并取得了成功的例子之一。在核内,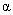 粒子受到核力吸引(负势能),但在核外, 粒子受到核力吸引(负势能),但在核外, 粒子将受到库仑力的排斥,这样,在核表面就形成一个势垒,如图16-10所示。若子核 粒子将受到库仑力的排斥,这样,在核表面就形成一个势垒,如图16-10所示。若子核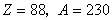 ,则可计算出 ,则可计算出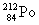 在 在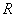 处的势垒高度约为 处的势垒高度约为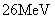 ,而212Po衰变时释放的 ,而212Po衰变时释放的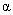 粒子动能为 粒子动能为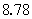 MeV,远低于势垒。按经典观点, MeV,远低于势垒。按经典观点,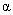 粒子不能跑出原子核,但按量子力学的势垒穿透理论,它有一定的概率逸出。由此计算得到的 粒子不能跑出原子核,但按量子力学的势垒穿透理论,它有一定的概率逸出。由此计算得到的 衰变平均寿命与 衰变平均寿命与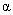 粒子动能的依赖关系,与实验给出的关系完全一致。这是量子力学用于原子核物理的首次成功的尝试,为量子力学初期的发展提供了有力的实验支持。 粒子动能的依赖关系,与实验给出的关系完全一致。这是量子力学用于原子核物理的首次成功的尝试,为量子力学初期的发展提供了有力的实验支持。
(2)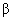 衰变 衰变
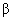 衰变是原子核改变其核电荷数 衰变是原子核改变其核电荷数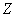 而质量数 而质量数 不变的自发衰变过程。在天然放射性中, 不变的自发衰变过程。在天然放射性中,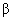 衰变都是发射电子的,叫 衰变都是发射电子的,叫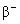 衰变;在人工制造的放射性核中,有放射性电子的 衰变;在人工制造的放射性核中,有放射性电子的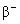 衰变,也有放射正电子的 衰变,也有放射正电子的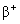 衰变。还有一种 衰变。还有一种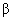 衰变过程,原子核吸收核外的轨道电子而改变其电荷数,这叫轨道电子俘获。 衰变过程,原子核吸收核外的轨道电子而改变其电荷数,这叫轨道电子俘获。
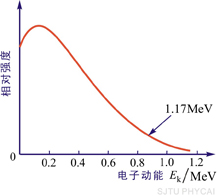
图16-11 Bi的 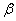 能谱  衰变是原子核放出高速电子。1914年查德威克就已测量了 衰变是原子核放出高速电子。1914年查德威克就已测量了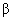 射线的能谱是连续的,1927年艾利斯和弗斯特精确地测量了 射线的能谱是连续的,1927年艾利斯和弗斯特精确地测量了 放射源 放射源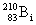 放出的热量。他们发现:原子核在 放出的热量。他们发现:原子核在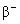 衰变过程中所放出电子的能量并不等于衰变前后原子核的能量差,而是从零到一个最大值有一定的分布,如图16-11所示。只有最大值的能量才恰好与衰变能量差相当。这引起了有关 衰变过程中所放出电子的能量并不等于衰变前后原子核的能量差,而是从零到一个最大值有一定的分布,如图16-11所示。只有最大值的能量才恰好与衰变能量差相当。这引起了有关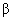 衰变是否遵从能量、动量守恒的争论。1933年,泡利为了解决这个问题,提出了中微子假说。他指出:“只有假定在 衰变是否遵从能量、动量守恒的争论。1933年,泡利为了解决这个问题,提出了中微子假说。他指出:“只有假定在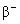 衰变过程中,伴随每一个电子有一个中性粒子(称之为中微子)一起被发射出来,使中微子和电子的能量之和为常数,才能解决连续 衰变过程中,伴随每一个电子有一个中性粒子(称之为中微子)一起被发射出来,使中微子和电子的能量之和为常数,才能解决连续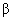 谱”。由于中微子既不带电,质量又近乎为零,在实验中就极难测量。我国科学家王淦昌先生于1942年首次提出通过 谱”。由于中微子既不带电,质量又近乎为零,在实验中就极难测量。我国科学家王淦昌先生于1942年首次提出通过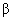 俘获(电子俘获)过程来从实验上探测中微子。直到1956年,Clyde Cowan和Frederick Reines才首次在实验中利用该方法找到中微子,以至Reines获得1995年诺贝尔物理学奖(Cowan于1974年去世)。1934年费米提出 俘获(电子俘获)过程来从实验上探测中微子。直到1956年,Clyde Cowan和Frederick Reines才首次在实验中利用该方法找到中微子,以至Reines获得1995年诺贝尔物理学奖(Cowan于1974年去世)。1934年费米提出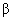 衰变理论,认为在原子核的 衰变理论,认为在原子核的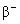 衰变过程中,是核内的中子转变为质子(留在核内)同时放出一个电子和一个中微子。后经进一步分析,确认与电子相关联的是反中微子 衰变过程中,是核内的中子转变为质子(留在核内)同时放出一个电子和一个中微子。后经进一步分析,确认与电子相关联的是反中微子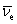 ,即 ,即
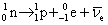
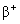 衰变可一般表示为 衰变可一般表示为
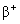 衰变是原子核放出正电子,同时伴随有中微子 衰变是原子核放出正电子,同时伴随有中微子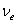 ,一般表示为 ,一般表示为
实际上在原子核内,质子也有一定的概率转变为中子(留在核内)同时放出一个正电子和一个中微子
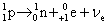
与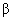 衰变相反的过程是电子俘获,即原子核俘获了与它最接近的内层电子,使核内的一个质子转变为中子,同时放出一个中微子。电子俘获一般表示为 衰变相反的过程是电子俘获,即原子核俘获了与它最接近的内层电子,使核内的一个质子转变为中子,同时放出一个中微子。电子俘获一般表示为
由于K层电子最靠近原子核,所以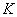 电子俘获最易发生。 电子俘获最易发生。
(3)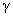 衰变 衰变
当原子核发生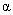 、 、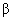 衰变时,往往衰变到子核的激发态。处于激发态的原子核是不稳定的,它要向低激发态或基态跃迁,同时放出 衰变时,往往衰变到子核的激发态。处于激发态的原子核是不稳定的,它要向低激发态或基态跃迁,同时放出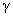 光子。处于激发态的原子核通过发射 光子。处于激发态的原子核通过发射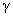 射线(即光子)而转变到较低能量状态或基态的过程称为 射线(即光子)而转变到较低能量状态或基态的过程称为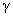 衰变。因此 衰变。因此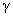 光子的能量为 光子的能量为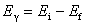 。例如,医学上治疗肿瘤最常用的放射源 。例如,医学上治疗肿瘤最常用的放射源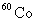 ,它的衰变如图16-12所示。 ,它的衰变如图16-12所示。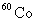 以 以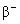 衰变到 衰变到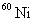 的 的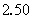 MeV激发态( MeV激发态(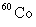 的 的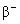 衰变的半衰期为 衰变的半衰期为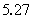 a)。 a)。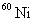 的激发态的寿命极短,它放出能量分别为 的激发态的寿命极短,它放出能量分别为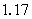 MeV和 MeV和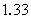 MeV两种 MeV两种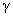 射线而跃迁到基态。 射线而跃迁到基态。
|






