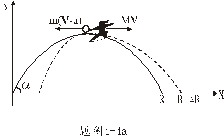
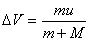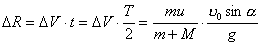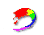 【例4-1】如题图4-1a所示,斜面长5米,高3米,斜面的下端与一水平面相接,一物块从斜面上端由静止开始下滑,物块与斜面及平面的摩擦系数均为 【例4-1】如题图4-1a所示,斜面长5米,高3米,斜面的下端与一水平面相接,一物块从斜面上端由静止开始下滑,物块与斜面及平面的摩擦系数均为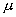 ,( ,(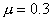 )。求物块从斜面顶端由静止开始下滑,滑到平面上后还能在平面上滑行多长距离?( )。求物块从斜面顶端由静止开始下滑,滑到平面上后还能在平面上滑行多长距离?(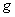 取10 取10 ) ) |
||
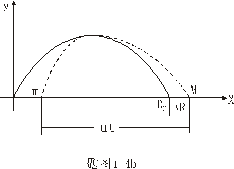
【解】设物块滑到斜面下端的速度大小为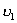 ,根据功能原理 ,根据功能原理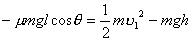 得 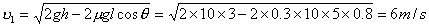 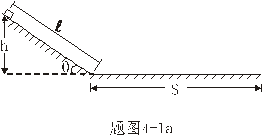 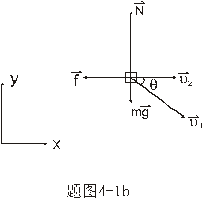 这里应注意的是 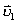 的方向是沿着斜面的,当物块通过转角处,速度变为水平方向,物体的动量发生了改变,则必定受到外力的冲量。 的方向是沿着斜面的,当物块通过转角处,速度变为水平方向,物体的动量发生了改变,则必定受到外力的冲量。参阅题图4-1b。在垂直方向( 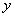 方向)应用动量原理: 方向)应用动量原理: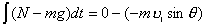 由于物体通过转角处的时间很短,物体与水平面碰撞瞬间的正压力 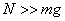 ,上式可写成: ,上式可写成: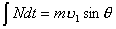 (1) (1)再在水平方向( 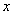 方向)上应用动量原理: 方向)上应用动量原理: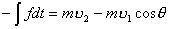 (2) (2)由于 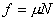 所以 所以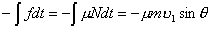 (3) (3)比较(2)、(3)式得: 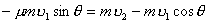 由此解得,得通过转角后,物块在水平面上开始运动的速度 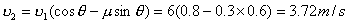 物块还能在水平面上滑行的距离 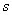 ,仍可用动能定理 ,仍可用动能定理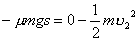 得 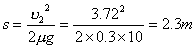 |
||
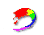 【例4-2】光滑的A玻璃弹子直径 【例4-2】光滑的A玻璃弹子直径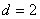 厘米,以速度 厘米,以速度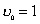 米/秒的速度与另一原来静止的完全相同的B玻璃弹子相撞,如题图a所示。运动弹子质心速度为 米/秒的速度与另一原来静止的完全相同的B玻璃弹子相撞,如题图a所示。运动弹子质心速度为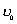 的方向偏离静止弹子球心距离 的方向偏离静止弹子球心距离 厘米,两弹子间的恢复系数 厘米,两弹子间的恢复系数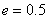 ,求碰撞后两弹子各速度为多少? ,求碰撞后两弹子各速度为多少? |
||
 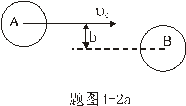
【解】取两弹子碰撞瞬时球心的连线方向为 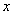 轴,垂直于连心线的方向为 轴,垂直于连心线的方向为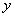 轴。(见题图b)由题意玻璃弹子光滑,所以两弹子在 轴。(见题图b)由题意玻璃弹子光滑,所以两弹子在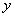 方向上的相互作用力为零,A玻璃弹子在 方向上的相互作用力为零,A玻璃弹子在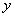 方向上的速度保持不变: 方向上的速度保持不变: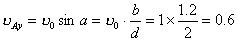 米/秒 米/秒在 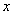 方向上,系统合外力为零,动量守恒: 方向上,系统合外力为零,动量守恒: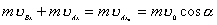 即: 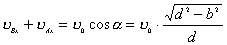 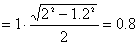 米/秒
(1) 米/秒
(1)又有恢复系数定义得: 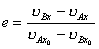 由题意知, 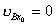 , ,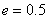 上式可改写为: 上式可改写为: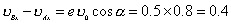 米/秒 (2) 米/秒 (2)
解(1)、(2)式得: 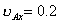 米/秒; 米/秒;
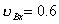 米/秒。 米/秒。由此知两球碰撞后的速度分别为: 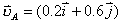 米/秒 米/秒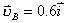 米/秒 米/秒
|
||
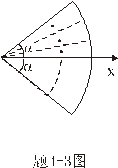
 【例4-3】试计算半径为R,顶角为 【例4-3】试计算半径为R,顶角为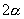 的匀质扇形板的质心位置。 的匀质扇形板的质心位置。 |
||
【解】我们先把大扇形分割成很多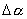 很小的顶角相同的小扇形,顶角很小的扇形就非常接近于三角形,三角形的质心位于中线的 很小的顶角相同的小扇形,顶角很小的扇形就非常接近于三角形,三角形的质心位于中线的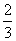 位置上,当顶角 位置上,当顶角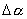 趋向于零时,各扇形的质心位于就分布在 趋向于零时,各扇形的质心位于就分布在 的圆弧上,因此我们求该扇形的质心只要求半径 的圆弧上,因此我们求该扇形的质心只要求半径 ,张角为 ,张角为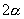 的匀质圆弧的质心即可。设这圆弧单位长度的质量为 的匀质圆弧的质心即可。设这圆弧单位长度的质量为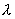 。 。
|
||
 【例4-4】质量为M的人,手里拿着质量为m的物体,此人用与地平线成 【例4-4】质量为M的人,手里拿着质量为m的物体,此人用与地平线成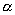 的速度 的速度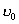 向前跳去,当他到达最高点时,把物体以相对于自己以速度u向后抛出,问由于物体的抛出,他跳过的距离与不抛物体时相比可增加多少? 向前跳去,当他到达最高点时,把物体以相对于自己以速度u向后抛出,问由于物体的抛出,他跳过的距离与不抛物体时相比可增加多少? |
||
方法二,质心坐标系中应用动量守恒定律: 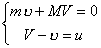 可得: 可得: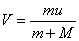 在下落时间 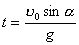 过程中,人相对于质心运动的距离,即为人比不抛出物体多跳过的距离: 过程中,人相对于质心运动的距离,即为人比不抛出物体多跳过的距离: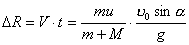 方法三,应用质心运动定律求解: 由于内力不改变质心原来运动的轨迹,由在质心C落地位置为人不抛出物体时原来落地位置,现人以相对于自己速度u 抛出物体m时,在下落时间 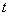 过程中,人M与物体m之间的距离: 过程中,人M与物体m之间的距离: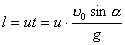 由质心位置公式知,质量为M的人离质心距离为: 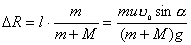 |
||
 【例4-5】如图所示,一质量为 【例4-5】如图所示,一质量为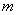 的匀质链条,长为L,手持其上端,下端与桌面接触。现使链条自静止释放落于桌面,试从下述三种不同的规律出发,计算链条下落 的匀质链条,长为L,手持其上端,下端与桌面接触。现使链条自静止释放落于桌面,试从下述三种不同的规律出发,计算链条下落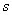 距离时桌面对链条的作用力: 距离时桌面对链条的作用力:(1)动量规律; (2)质心运动规律; (3)变质量动力学规律; |
||
【解】这是一个连续分布的柔性质点系,可以选择不同的部分作为研究对象,也可以从不同的角度求解。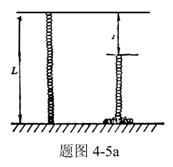 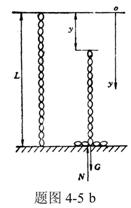 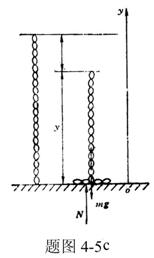 方法一,运用动量规律求解。取如图b坐标。设 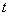 时刻下落至桌面部分的链条长为 时刻下落至桌面部分的链条长为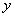 ,质量为 ,质量为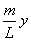 ; ;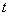 至 至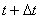 时间内落到桌面上的链条质量为 时间内落到桌面上的链条质量为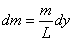 ,其速度由 ,其速度由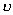 减到0。选取已下落至桌面以及 减到0。选取已下落至桌面以及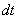 时间内下落至桌面的 时间内下落至桌面的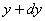 段链条为研究对象。由于链条自由下落, 段链条为研究对象。由于链条自由下落,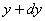 段仅受到重力 段仅受到重力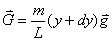 和桌面支撑力 和桌面支撑力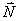 的作用,根据质点系动量定理: 的作用,根据质点系动量定理: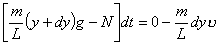 略去 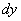 段重力,得: 段重力,得: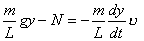 因 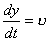 , ,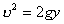 ,代入上式,且按题意 ,代入上式,且按题意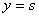 ,解得: ,解得: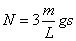 。 。可见链条下落时对桌面的冲击力为已下落至桌面上链条重量的两倍。 方法二,运用质心运动规律求解。由于整条链条受重力和桌面支撑力的作用,其质心作加速运动。选取如图c所示的坐标,以整条链条为研究对象。 质心位置: 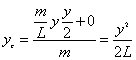 质心速度: 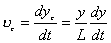 质心加速度: 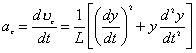 且: 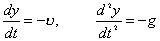 , 代入上式有: , 代入上式有: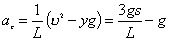 根据质心运动定理: 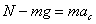 解得: 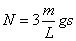 方法三,运用变质量动力学规律求解。取下落至桌面部分的链条为研究主体,其质量 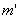 逐渐增加,对如图b坐标,质量流相对主体速度大小: 逐渐增加,对如图b坐标,质量流相对主体速度大小: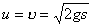 质量流: 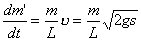 质量流对主体的推力: 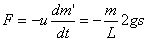 主体在其重力、桌面支撑力和质量流对主体的推力作用下保持静止。根据变质量动力学方程: 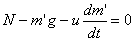 , ,同样得到上述结果。 |
 【例4-6】从地球表面沿与铅垂线成 【例4-6】从地球表面沿与铅垂线成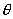 角的方向发射一抛射体初速度 角的方向发射一抛射体初速度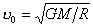 ,式中M、R分别为地球的质量和半径。若忽略空气阻力和地球自转的影响,试求: ,式中M、R分别为地球的质量和半径。若忽略空气阻力和地球自转的影响,试求:(1)抛射体上升的最大高度H和射程的直线距离AD; (2)求飞行时间T。 |
|
【解】(1)由于发射速度比较大,飞行高度与地球半径可比较,见图a。抛射体在飞行过程中受到的引力大小和方向都在改变,可以证明其运动轨迹不再是抛物线,而是椭圆。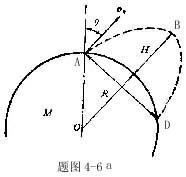 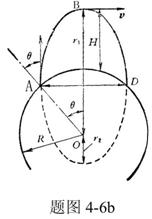 抛射体受地球引力作用,对地心的力矩为零,抛射体对地心的角动量守恒。在发射地A和最大高度B处的角动量满足: 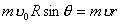 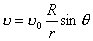 (1) (1)物体只在地球引力作用下运动,系统的机械能守恒: 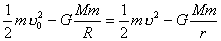 (2) (2)将  , , 和(1)式代入(2)式,则(2)式简化为: 和(1)式代入(2)式,则(2)式简化为: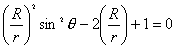 该二次三项式的解为: 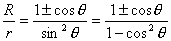 , ,解得: 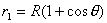 椭圆的远地点, 椭圆的远地点,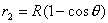 椭圆的近地点。 椭圆的近地点。椭圆的长半轴和短半轴分别为: 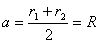 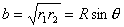 (3) (3)由图b可见,抛射体的发射点和落地点正处在椭圆短半轴的端点上,抛射体飞行的最大高度和射程的直线距离分别为: 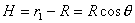 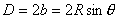 例如沿 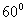 角方向发射,抛射体可达到的最大高度为: 角方向发射,抛射体可达到的最大高度为: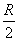 。 。(2)由图b所示抛射体的飞行的面积速度: 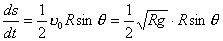 从发射点到落地点抛射体扫过的面积为半椭圆和一三角形OAD面积之和,即: 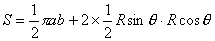 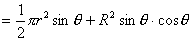 由开普勒第二定律得抛射体的飞行时间: 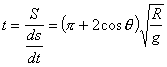 若 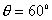 ,则飞行时间 ,则飞行时间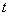 为 为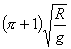 。 。 |
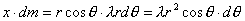
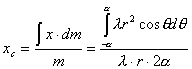
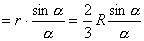
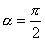 ,代入上式即可:
,代入上式即可: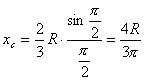
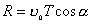
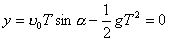
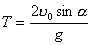 (
(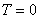 删去)
删去)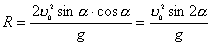
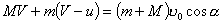
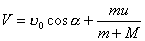
 增加了速度:
增加了速度: