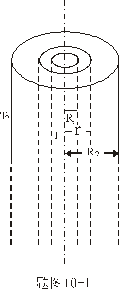
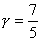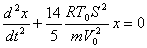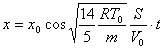 【例10-1】两个无限长圆筒共轴地套在一起,内筒和外筒半径分别为 【例10-1】两个无限长圆筒共轴地套在一起,内筒和外筒半径分别为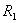 和 和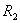 ,内筒和外筒间保持恒定的温度 ,内筒和外筒间保持恒定的温度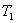 和 和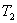 ,且 ,且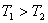 。已知两筒间物质的热传导系数为 。已知两筒间物质的热传导系数为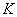 ,试求稳定状态时: ,试求稳定状态时:
(1)单位时间内筒放出的热量
(2)在离轴线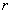 处( 处(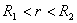 )的温度 )的温度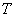 。 。 |
【解】(1)根据热传导实验定律:
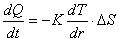 (1) (1)
由稳定条件可知,两筒间任一区域温度分布都保持不变,也就是流入这区域的热量与流出的热量必相等。取上式中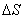 为一圆柱面 为一圆柱面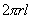 。介于 。介于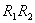 之间的任何圆柱面单位时间流过的热量均相等,即(1)式中的 之间的任何圆柱面单位时间流过的热量均相等,即(1)式中的 为常数。 为常数。
(1)式可写成: 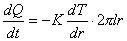
分离变量再积分: 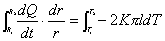
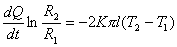
即: 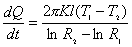 (2) (2)
(2)设在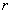 处的温度为 处的温度为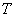 ,同样由热传导公式(1)可导得类似于(2)的表达式: ,同样由热传导公式(1)可导得类似于(2)的表达式:
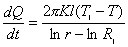 (3) (3)
由(2)、(3)式可解得: 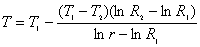 |
 |
|
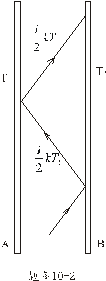
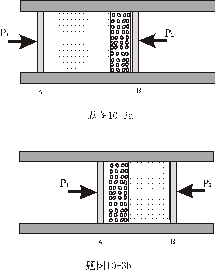
 【例10-2】图中A、B为保温瓶两胆壁,两壁间抽空后存有摩尔质量为M的低压气体,气体单位体积的质量为 【例10-2】图中A、B为保温瓶两胆壁,两壁间抽空后存有摩尔质量为M的低压气体,气体单位体积的质量为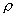 。其分子自由程远大于壁间距。若内壁A的温度为 。其分子自由程远大于壁间距。若内壁A的温度为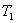 ,外壁B的温度为 ,外壁B的温度为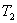 ,分子与壁碰撞后即获得与该壁温度相当的平均能量 ,分子与壁碰撞后即获得与该壁温度相当的平均能量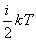 。试证低气压的热传导系数为 。试证低气压的热传导系数为 。 。 |
【解】两壁间的分子分别给单位面积器壁碰撞的分子数为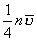 ,分子与内外壁各碰撞一次,就输运一份 ,分子与内外壁各碰撞一次,就输运一份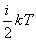 的热量,所以单位时间分子给内外壁之间传递的热量: 的热量,所以单位时间分子给内外壁之间传递的热量:
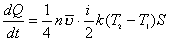
式中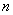 为单位体积中的分子数,即 为单位体积中的分子数,即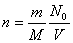 ,再注意到 ,再注意到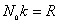 ,及 ,及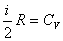 上式可写成: 上式可写成:
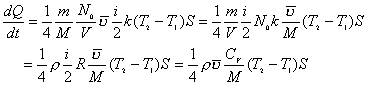
由此可得证低气压热传导系数:  |
 |
|
 【例10-3】图为一绝热管,中间有一固定多孔塞,其作用是允许气体缓慢通过,多孔塞的两边各有一个绝热活塞。开始活塞A和多孔塞间装有1mol的双原子气体,活塞B紧靠多孔塞。在多孔塞两边保持恒定的压力差 【例10-3】图为一绝热管,中间有一固定多孔塞,其作用是允许气体缓慢通过,多孔塞的两边各有一个绝热活塞。开始活塞A和多孔塞间装有1mol的双原子气体,活塞B紧靠多孔塞。在多孔塞两边保持恒定的压力差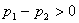 ,气体缓慢地从左边流到右边。 ,气体缓慢地从左边流到右边。
(1)若是理想气体,在节流膨胀过程中,气体熵的变化多大?
(2)若是实际气体,只考虑体积修正,在节流膨胀过程中,气体温度的变化多大? |
【解】(1)由热力学第一定律
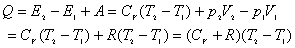
由题意在这节流膨胀过程中系统与外界绝热,所以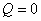 ,得: ,得:
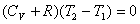
即 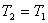
在此过程中,注意到系统初态终态温度不变,系统的熵变:
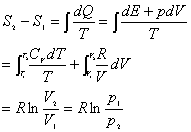
(2)根据题意,只考虑体积的修正量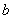 ,则范氏方程可写成: ,则范氏方程可写成:
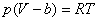 或 或
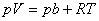
再将热力学第一定律应用于该过程
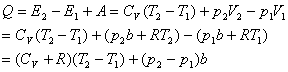
由于系统与外界绝热,上式为0,即
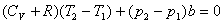
得 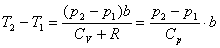
题中表明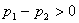 ,得 ,得
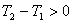
即温度升高。其物理意义是本题仅考虑斥力修正量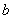 ,在体积膨胀过程中斥力的弹性势能作正功,弹性势能减少,而分子动能增加,因此系统经过此节流过程温度升高。 ,在体积膨胀过程中斥力的弹性势能作正功,弹性势能减少,而分子动能增加,因此系统经过此节流过程温度升高。 |
 |
|
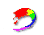 【例10-4】某空调装置,连续运转时功率为 【例10-4】某空调装置,连续运转时功率为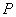 ,它吸取室内低温 ,它吸取室内低温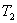 处的热量向室外高温 处的热量向室外高温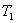 处送去,由于室内外温差,单位时间内室外又有热量 处送去,由于室内外温差,单位时间内室外又有热量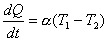 传入室内。若空调装置可看作理想卡诺机,并已知 传入室内。若空调装置可看作理想卡诺机,并已知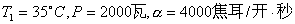 。求稳定状态时室内的最低温度 。求稳定状态时室内的最低温度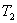 为多少? 为多少? |
【解】由卡诺机的制冷系数
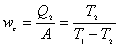
可得: 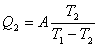
稳定状态时,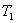 、 、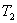 为常量,上式对时间求导后 为常量,上式对时间求导后
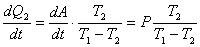 (1) (1)
而单位时间内室外传入室内的热量
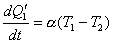 (2) (2)
稳定状态时应满足
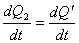
即: 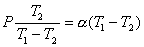
或: 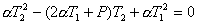
解此方程得:
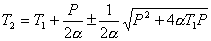
空调机取暖时取“+”,致冷时取“—”号,代入数据:
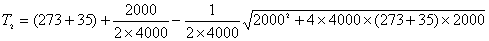
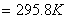
即: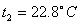
|
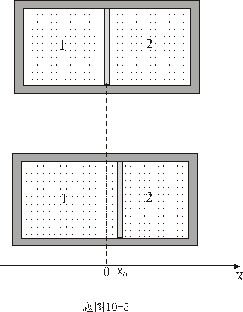
 【例10-5】一绝热容器中间被一质量为 【例10-5】一绝热容器中间被一质量为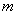 的绝热活塞分成容积均为 的绝热活塞分成容积均为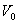 的两部分,两边各装有温度均为 的两部分,两边各装有温度均为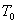 的一摩尔双原子理想气体,若将活塞向右略偏移 的一摩尔双原子理想气体,若将活塞向右略偏移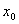 ,然后放手,问活塞以后如何运动?并写出其运动方程。(摩擦忽略不计) ,然后放手,问活塞以后如何运动?并写出其运动方程。(摩擦忽略不计) |
【解】由于容器与活塞都是绝热的,左边容器1,和右边容器2,在运动过程中都满足绝热过程方程。
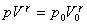
将上式微分:
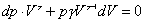
得 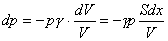
由于题设最大偏移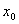 很小,所以任意位置处1室产生的压强改变量近似于 很小,所以任意位置处1室产生的压强改变量近似于
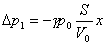
同理2室引起的压强改变量:
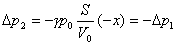
左右两容器内气体对活塞的合力
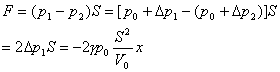
根据牛顿动力学方程
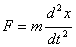
可得 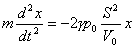
即
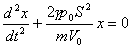
考虑到理想气体状态方程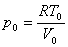 及双原子理想气体的热容比 及双原子理想气体的热容比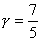
代入上式得: 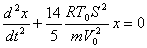
由此得活塞的谐振动方程
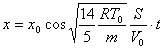
|
 |
|
| |
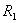 和
和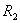 ,内筒和外筒间保持恒定的温度
,内筒和外筒间保持恒定的温度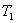 和
和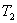 ,且
,且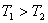 。已知两筒间物质的热传导系数为
。已知两筒间物质的热传导系数为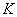 ,试求稳定状态时:
,试求稳定状态时:
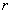 处(
处(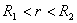 )的温度
)的温度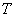 。
。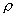 。其分子自由程远大于壁间距。若内壁A的温度为
。其分子自由程远大于壁间距。若内壁A的温度为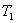 ,外壁B的温度为
,外壁B的温度为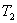 ,分子与壁碰撞后即获得与该壁温度相当的平均能量
,分子与壁碰撞后即获得与该壁温度相当的平均能量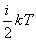 。试证低气压的热传导系数为
。试证低气压的热传导系数为 。
。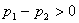 ,气体缓慢地从左边流到右边。
,气体缓慢地从左边流到右边。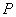 ,它吸取室内低温
,它吸取室内低温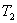 处的热量向室外高温
处的热量向室外高温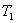 处送去,由于室内外温差,单位时间内室外又有热量
处送去,由于室内外温差,单位时间内室外又有热量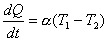 传入室内。若空调装置可看作理想卡诺机,并已知
传入室内。若空调装置可看作理想卡诺机,并已知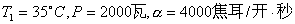 。求稳定状态时室内的最低温度
。求稳定状态时室内的最低温度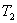 为多少?
为多少?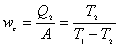
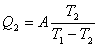
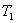 、
、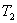 为常量,上式对时间求导后
为常量,上式对时间求导后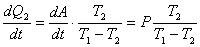 (1)
(1)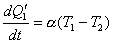 (2)
(2)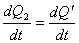
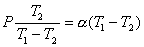
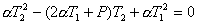
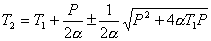
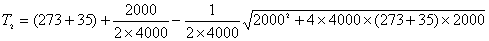
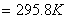
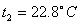
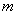 的绝热活塞分成容积均为
的绝热活塞分成容积均为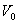 的两部分,两边各装有温度均为
的两部分,两边各装有温度均为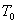 的一摩尔双原子理想气体,若将活塞向右略偏移
的一摩尔双原子理想气体,若将活塞向右略偏移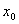 ,然后放手,问活塞以后如何运动?并写出其运动方程。(摩擦忽略不计)
,然后放手,问活塞以后如何运动?并写出其运动方程。(摩擦忽略不计)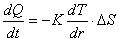 (1)
(1)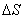 为一圆柱面
为一圆柱面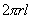 。介于
。介于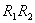 之间的任何圆柱面单位时间流过的热量均相等,即(1)式中的
之间的任何圆柱面单位时间流过的热量均相等,即(1)式中的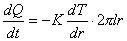
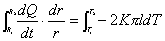
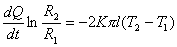
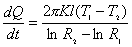 (2)
(2)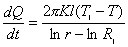 (3)
(3)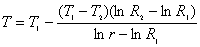

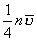 ,分子与内外壁各碰撞一次,就输运一份
,分子与内外壁各碰撞一次,就输运一份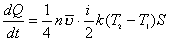
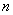 为单位体积中的分子数,即
为单位体积中的分子数,即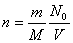 ,再注意到
,再注意到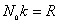 ,及
,及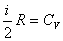 上式可写成:
上式可写成: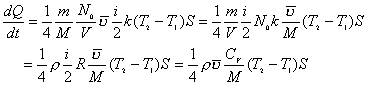

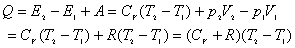
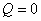 ,得:
,得: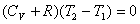
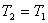
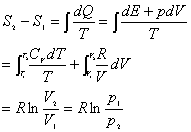
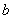 ,则范氏方程可写成:
,则范氏方程可写成: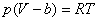 或
或
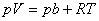
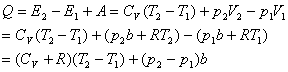
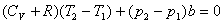
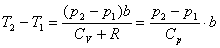
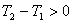

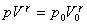
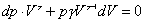
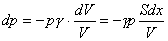
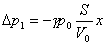
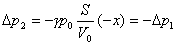
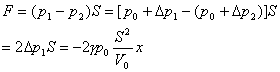
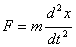
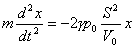
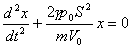
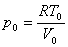 及双原子理想气体的热容比
及双原子理想气体的热容比