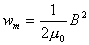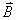
|
|||||||||||||||||||||
运动电荷或载流导线在空间激发的磁场性质的物理量称为磁感应强度,它的大小定义为 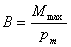 式中 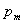 为试验线圈的磁矩, 为试验线圈的磁矩,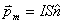 。 。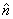 为试验线圈面积S的法向单位矢量。 为试验线圈面积S的法向单位矢量。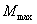 是试验线圈在试验位置上所受到的最大磁力矩,磁感应强度的方向就是试验线圈平衡位置的磁矩 是试验线圈在试验位置上所受到的最大磁力矩,磁感应强度的方向就是试验线圈平衡位置的磁矩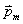 的方向。 的方向。或 B的定义为: 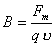 式中 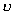 为运动电荷 为运动电荷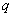 在该点的速度量值, 在该点的速度量值,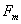 为运动电荷在该点受到的最大磁力。 为运动电荷在该点受到的最大磁力。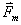 、 、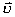 、 、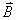 遵守右手螺旋法则。 遵守右手螺旋法则。磁感应强度的单位为1特斯拉=1韦伯 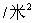 = =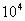 高斯。 高斯。 |
|||||||||||||||||||||
|
|||||||||||||||||||||
 三、运动电荷产生的磁场 三、运动电荷产生的磁场 |
|||||||||||||||||||||
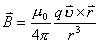 它的大小:
它的大小: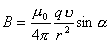 它的方向由 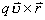 确定。 确定。 |
|||||||||||||||||||||
 四、安培环路定律 四、安培环路定律 |
|||||||||||||||||||||
在磁场中,沿任何闭合曲线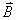 矢量的线积分等于真空中的磁导率 矢量的线积分等于真空中的磁导率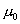 乘以包围在这闭合曲线内各电流的代数和,其数学表达式为 乘以包围在这闭合曲线内各电流的代数和,其数学表达式为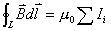 应用安培环路定律时应注意:闭合路在 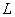 上的 上的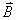 是空间所有电流产生的总的磁感应强度;沿闭合曲线 是空间所有电流产生的总的磁感应强度;沿闭合曲线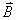 矢量线积分,等于 矢量线积分,等于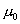 乘以被闭合曲线 乘以被闭合曲线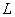 所包围的电流代数和而与闭合曲线外的电流无关;电流方向与回路方向成右手系的取正,成左手系的取负;安培环流定律是一普遍规律,但要用安培环流定律来求磁感应强度,那么空间电流的分布必须要具有特殊的对称性。 所包围的电流代数和而与闭合曲线外的电流无关;电流方向与回路方向成右手系的取正,成左手系的取负;安培环流定律是一普遍规律,但要用安培环流定律来求磁感应强度,那么空间电流的分布必须要具有特殊的对称性。1、无限长直圆柱形均匀载流导线内外的磁场 载流导线内 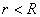 : :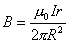 载流导线外 载流导线外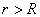 : :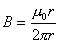 2、螺绕环所产生的磁场 螺绕环内: 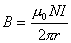 螺线环外:
螺线环外: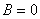 当环形螺绕管截面很小时,即截面线度远小于环的平均半径时 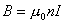 。相当于长直螺线管。 。相当于长直螺线管。
|
|||||||||||||||||||||
由于磁感应线是闭合曲线,因此通过任一闭合曲面的磁通量必然为零。这就是磁场中的高斯定理,它的数学表达式为: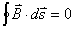 它表明了磁场是个涡旋场,不存在磁荷。 |
|||||||||||||||||||||
1、安培定律 电流元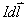 在磁感应强度为 在磁感应强度为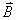 的磁场中所受到的安培力: 的磁场中所受到的安培力: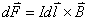 。 。2、通电线圈在磁感应强度均匀为 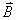 的磁场中所受到的磁力矩 的磁场中所受到的磁力矩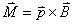 式中 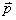 为线圈的磁矩等于 为线圈的磁矩等于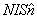 。 。3、磁力的功 不论通电导线所受的磁场力的功 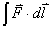 还是通电线圈在磁力矩作用下所作的功 还是通电线圈在磁力矩作用下所作的功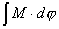 ,都可以表示为 ,都可以表示为
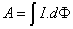 如果导线或线圈运动过程中它们的电流 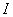 不变,那么磁力所作的功只需电流 不变,那么磁力所作的功只需电流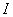 乘上磁通量的变化 乘上磁通量的变化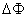 即可,即 即可,即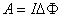 |
|||||||||||||||||||||
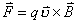 式中可知 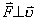 ,所以洛仑兹力不作功。 ,所以洛仑兹力不作功。带电粒子在均匀场磁内运动的规律: 1、带电粒子运动的速度 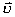 与磁感应强度 与磁感应强度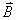 的方向平行时,带电粒子受到的洛仑兹力为零。粒子将作匀速直线运动。 的方向平行时,带电粒子受到的洛仑兹力为零。粒子将作匀速直线运动。2、带电为 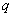 的粒子的速度 的粒子的速度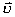 与 与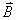 的方向垂直时,粒子将作圆周运动,可以根据 的方向垂直时,粒子将作圆周运动,可以根据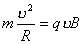 的关系求得带电粒子运动的轨迹半径 的关系求得带电粒子运动的轨迹半径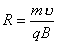 ,带电粒子运动的周期 ,带电粒子运动的周期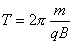 。 。3、带电 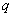 的粒子速度 的粒子速度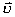 与 与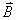 的方向成 的方向成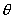 角时,粒子将作匀速螺旋运动,螺旋线的半径 角时,粒子将作匀速螺旋运动,螺旋线的半径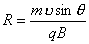 ,粒子运动的周期 ,粒子运动的周期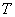 仍为 仍为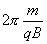 ,螺距 ,螺距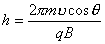 。 。 |
|||||||||||||||||||||
把一载流导体放在磁场中,如果磁场方向与电流方向垂直,由于导体中的载流子,受到洛仑兹力的作用而发生横向漂移,在磁场和电流二者垂直的方向上出现横向电势差,这一现象叫霍耳效应,霍耳电势差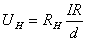 其中 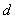 是在磁场方向上霍耳元件的厚度, 是在磁场方向上霍耳元件的厚度,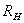 是霍耳系数,它仅与霍耳元件的材料有关,且 是霍耳系数,它仅与霍耳元件的材料有关,且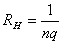 (或 (或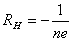 )霍耳系数实际就是霍耳元件的载流子浓度的倒数。 )霍耳系数实际就是霍耳元件的载流子浓度的倒数。 |
|||||||||||||||||||||
|
|||||||||||||||||||||
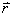 位置处所激发的磁感应强度
位置处所激发的磁感应强度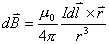
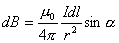
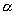 是
是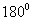 的夹角,
的夹角,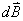 的方向由
的方向由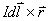 所确定。
所确定。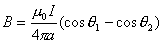
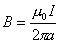
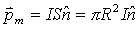 叫线圈的磁矩。
叫线圈的磁矩。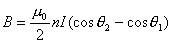
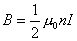 或
或
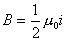
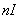 和
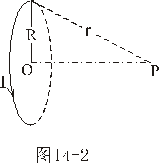
和 都表示单位宽度电流强度。
都表示单位宽度电流强度。 
 或
或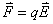
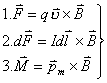 三种方式定义的
三种方式定义的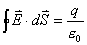
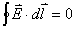
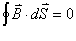
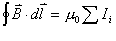
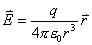
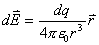
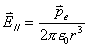 ;
;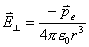
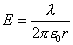
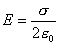
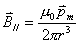 ;
;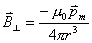
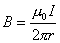
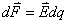
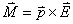
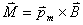
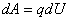 (
(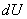 为电势的改变)
为电势的改变)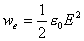
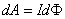 (
(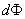 为磁通量的改变)
为磁通量的改变)