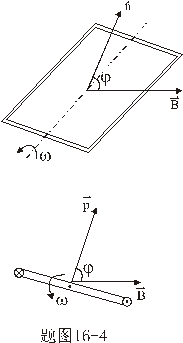
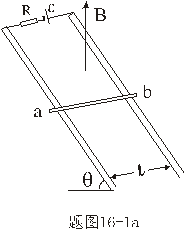
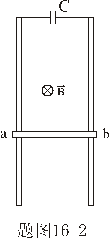
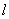 ,导轨与水平面成 ,导轨与水平面成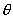 角放置,整个装置处在磁感应强度均匀为 角放置,整个装置处在磁感应强度均匀为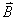 的磁场之中, 的磁场之中,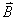 的方向垂直地面向上,两导轨间串接了电阻R及电动势为 的方向垂直地面向上,两导轨间串接了电阻R及电动势为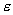 的电源。滑杆ab质量为m,滑杆初速为零,求滑杆下滑速度随时间的关系。并由此求滑杆的极限速度。 的电源。滑杆ab质量为m,滑杆初速为零,求滑杆下滑速度随时间的关系。并由此求滑杆的极限速度。 |
||
 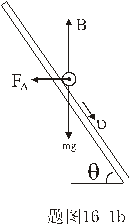 【解】滑杆在下滑过程中除受重力之外还受到安培力的作用,这里应注意到安培力 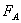 的方向不是沿斜面方向,而是垂直于B与杆ab组成的平面,见图16-1b,由此列出牛顿运动方程: 的方向不是沿斜面方向,而是垂直于B与杆ab组成的平面,见图16-1b,由此列出牛顿运动方程: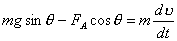 (1) (1)流过滑杆ab的电流除了电源电动势 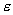 的作用,还要考虑滑杆本身产生的感生电动势 的作用,还要考虑滑杆本身产生的感生电动势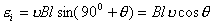 由判别可知 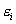 的方向与 的方向与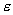 相同,所以流过滑杆ab的电流 相同,所以流过滑杆ab的电流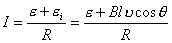 由此得安培力 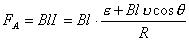 (2) (2)将(2)式代入(1)式得: 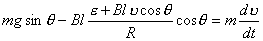 (3) (3)分离变量积分: 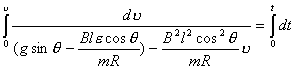 可得 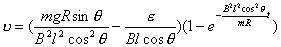 当 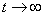 时滑杆到达极限速度 时滑杆到达极限速度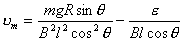 如果只要求极限速度 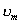 的话,那么 的话,那么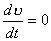 的条件直接代入(3)就可求得。 的条件直接代入(3)就可求得。 |
||
|
||
 ,并维持以圆形的方式收缩,设导线非常柔软,忽略导线的质量,问需要多长的时间圆形部分完全闭合? ,并维持以圆形的方式收缩,设导线非常柔软,忽略导线的质量,问需要多长的时间圆形部分完全闭合? |
||
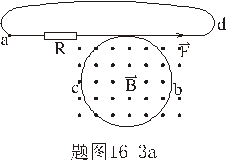 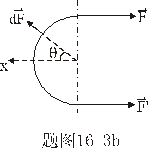 【解】由于圆圈形导线在收缩过程中,通过圆圈形面积上的磁通量减少,线圈内要产生感应电流 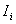 。感应电流在磁场中就要受到安培力,安培力方向可以判别是沿半径方向向外,由于忽略导线质量,导线所受的外力F,导线张力F'与安培力三者平衡,如图16-3b所示,并如图取坐标,电流元 。感应电流在磁场中就要受到安培力,安培力方向可以判别是沿半径方向向外,由于忽略导线质量,导线所受的外力F,导线张力F'与安培力三者平衡,如图16-3b所示,并如图取坐标,电流元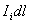 所受的安培力在x方向上的分量: 所受的安培力在x方向上的分量: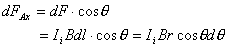 由于对称性,半圆弧产生的安培力合力 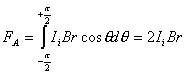 由对称性及力平衡条件 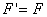 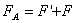 得: 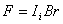 (1) (1)由于外力作用,r在收缩过程中回路内产生的感应电流: 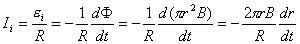 将 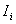 代入(1)式得: 代入(1)式得: 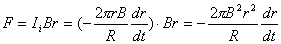 得: 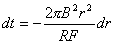 由初始条件 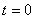 , ,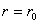 , ,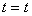 , ,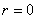 两边积分 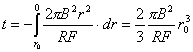 |
||
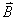 的均匀磁场内,有一面积为S的矩形线框,线框回路的电阻为R(忽略自感),线框绕其对称轴OO'以匀角速度 的均匀磁场内,有一面积为S的矩形线框,线框回路的电阻为R(忽略自感),线框绕其对称轴OO'以匀角速度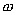 旋转(如题图16-4所示)。 旋转(如题图16-4所示)。(1)求在如图位置时线框所受的磁力矩为多大? (2)为维持线框匀角速度转动,外力矩对线框每转一周需作的功为多少? |
||
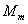 平衡,就是 平衡,就是
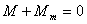 或 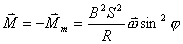 外力矩对线框每转一周所作的功: 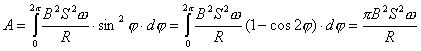 方法二,外力所作的正功与磁力所作的负功大小相等时线框将维持匀角速转动。我们计算磁力所作的功  将(1)式中的  和(3)式代入上式,得 和(3)式代入上式,得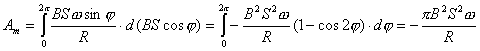 这里应注意到磁力的功不能用 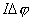 来计算,因为线框转动一周 来计算,因为线框转动一周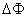 为零,但在转动过程中感应电流 为零,但在转动过程中感应电流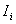 不是常量,所以必须用上述积分来计算。所以外力矩的功 不是常量,所以必须用上述积分来计算。所以外力矩的功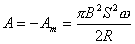 方法三,用能量守恒定律来解,外力矩作了功,绕框旋转一周后,其它状态没有产生变化,只是感生电动势和感生电流在绕框中产生焦耳楞次热。交流电一个周期所产生的焦耳热就是外力矩所作的功。即: 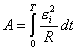 将(2)式代入上式得 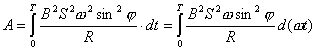 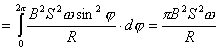 若需计算外力矩的平均功率,则 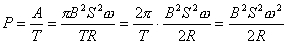 上式实际上也就是交流电输出的功率。 |
||
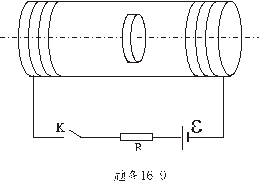
 (内阻不计,纯电感L及 (内阻不计,纯电感L及 、 、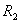 均为已知)。在电路 均为已知)。在电路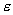 、L、 、L、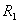 到达稳定状态的时候,将开关K合上,求: 到达稳定状态的时候,将开关K合上,求:(1) 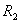 两端的电压随时间的变化; 两端的电压随时间的变化;(2)K合上长时间后K再断开,求 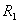 两端电压随时间的变化。 两端电压随时间的变化。 |
||
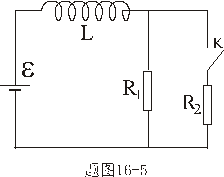 【解】(1)K合上任一时刻,电路微分方程为: 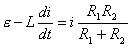 分离变量并积分,注意到电感上的电流不能突变。 初始条件 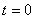 流过电感L的电流 流过电感L的电流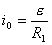 , ,将上式分离变量后积分: 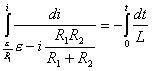 积分得: 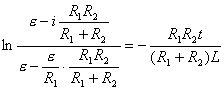 即: 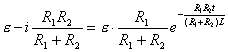 式中 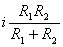 即为 即为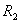 两端的电压U,所以 两端的电压U,所以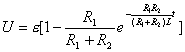 (2)断开 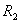 后任一时刻电路微分方程为: 后任一时刻电路微分方程为: 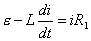 分离变量并积分,并注意到电感中的电流不能突变,这里的 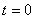 的 的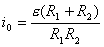 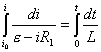 积分得: 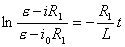 得: 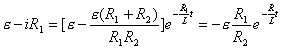 此式中的 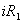 即为 即为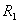 两端的电压 两端的电压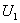 ,移项后得: ,移项后得: 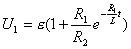 由此结果可知,当开关K断开瞬时( 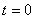 )电阻 )电阻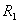 两端的电压 两端的电压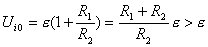 如 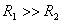 时, 时,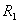 两端就会产生很高的电压,如果 两端就会产生很高的电压,如果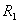 是电压表或者晶体管元件,如未加保护措施,则很可能会损坏电路元件,因此在有电感元件的电路里要特别注意。 是电压表或者晶体管元件,如未加保护措施,则很可能会损坏电路元件,因此在有电感元件的电路里要特别注意。
|
||
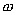 绕y轴匀速转动,铜圈所在处磁感应强度均匀为B,方向沿x轴正向。 绕y轴匀速转动,铜圈所在处磁感应强度均匀为B,方向沿x轴正向。(1)开始时 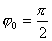 ,铜圈中电流为零,求铜圈中任一时刻中的电流 ,铜圈中电流为零,求铜圈中任一时刻中的电流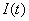 ; ;(2)求当铜圈中的法线 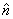 从 从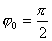 到 到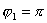 转过 转过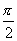 的过程中磁力的功。 的过程中磁力的功。 |
||
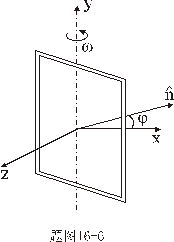 【解】(1)方法一,由铜环回路内应用基尔霍夫回路电压定律。 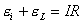 式中感应电动势 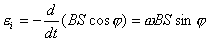 ,自感电动势 ,自感电动势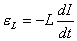 。由题设铜圈电阻很小可忽略不计,即 。由题设铜圈电阻很小可忽略不计,即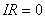 。因此上式可写成: 。因此上式可写成: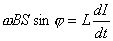 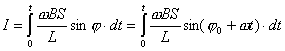 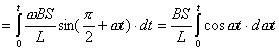 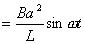 方法二,铜圈内的总磁通量: 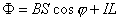 铜圈环路内总的感应电动势 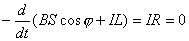 即:  由初始条件 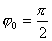 , ,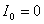 代入上式得恒量为零 代入上式得恒量为零即: 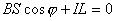 得: 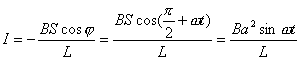 (2)方法一,铜圈所受的磁力矩的大小 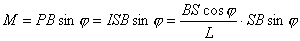 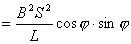 磁力矩的方向( 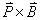 的方向)与 的方向)与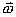 方向相反,这力矩所作的功 方向相反,这力矩所作的功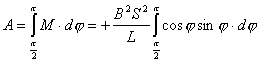 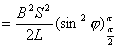 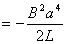 方法二,磁力矩所作的功 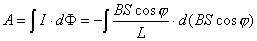 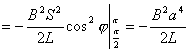 方法三,磁力所作的功为磁场能的减少 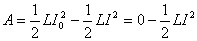 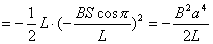
|
||
 和 和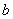 ,以初速 ,以初速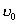 沿x轴正方向运动。当 沿x轴正方向运动。当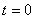 进入磁感应强度为 进入磁感应强度为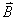 的匀强磁场,如图16-7a所示。磁场方向与 的匀强磁场,如图16-7a所示。磁场方向与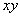 平面垂直,充满 平面垂直,充满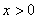 的空间。设线框的自感系数为L,质量为 的空间。设线框的自感系数为L,质量为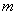 。 。(1)求  时线框中的电流变化率; 时线框中的电流变化率;(2)讨论线框的运动规则。 |
||
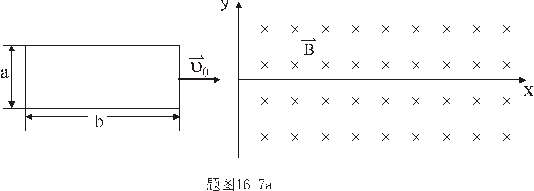 【解】设  (1)线框回路电压方程 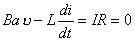 (题设导体电阻可忽略不计,取R=0) (题设导体电阻可忽略不计,取R=0)因为 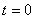 , ,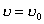 ,所以有 ,所以有 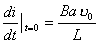 (2)首先讨论线框电流随位置或时间的变化规律,由回路电压方程: 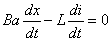 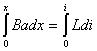 得: 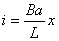 其次讨论在安培力作用下的线框运动规律:可以判别安培力的方向始终于线框运动的速度方向相反,得: 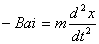 即: 即:
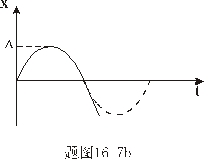
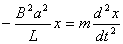 得: 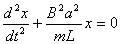 此为谐振动方程,它的解为: 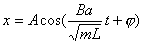 由初始条件 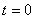 , ,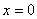 , ,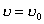 ,可确定 ,可确定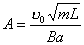 , ,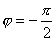 ,得: ,得: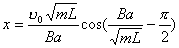 讨论: (1)若 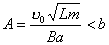 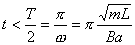 ,线框的运动为谐振动, ,线框的运动为谐振动,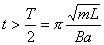 ,线框回到 ,线框回到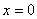 处以 处以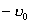 离开磁场区它的运动图线如图16-7b所示。 离开磁场区它的运动图线如图16-7b所示。(2)若 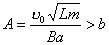 ,当 ,当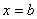 时,线框全部进入磁场,线框的磁通量不再变化,此后线框不再受安培力作用,将以此时的速度作匀速直线运动。运动图线如图16-7c所示。 时,线框全部进入磁场,线框的磁通量不再变化,此后线框不再受安培力作用,将以此时的速度作匀速直线运动。运动图线如图16-7c所示。
 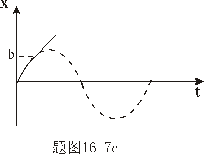 |
||
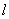 ,如图所示。若两螺线管各自通电后产生的磁场分别为 ,如图所示。若两螺线管各自通电后产生的磁场分别为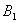 和 和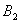 ,忽略边缘效应,试求: ,忽略边缘效应,试求:(1)两螺线管的互感磁能; (2)两螺线管的相互作用力。 |
||
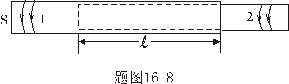 【解】(1)方法一,将螺线管分为左、中、右三段,其磁感应强度分别为 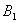 、 、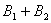 和 和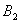 ,螺线管中的总磁能 ,螺线管中的总磁能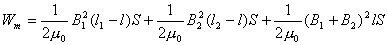 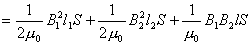 可见上式中第一项为螺线管1的自感磁能,第二项为螺线管2的自感磁能,第三项为两螺线管互感磁能,即 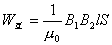 如果两螺线管绕向相反,其磁感应强度方向相反,互感磁能出现负值,而自感磁能总是正的。 方法二,螺线管1中电流的磁感应线通过螺线管2的磁通链数 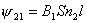 ,两螺线管的互感系数 ,两螺线管的互感系数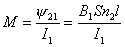 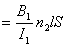 互感磁能 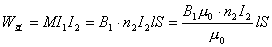 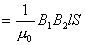 (2)两螺线管相向位移为 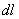 时,由于互感系数变化,产生互感电动势。电源要维持两螺线管中电流不变,必须克服互感电动势做功。电源所做的功转变为互感磁能的增加和磁力的功。 时,由于互感系数变化,产生互感电动势。电源要维持两螺线管中电流不变,必须克服互感电动势做功。电源所做的功转变为互感磁能的增加和磁力的功。两电源克服互感电动势做功分别为: 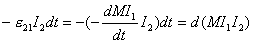  两电源克服互感电动势所作的功为 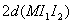 ,而互感磁能的增加为 ,而互感磁能的增加为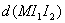 ,磁场力所做的功为 ,磁场力所做的功为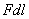 。根据功能关系 。根据功能关系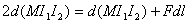 得: 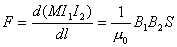 |
||
 回路电阻为R的电路中(如图16-9所示),求开关K接通长时间后,带电圆盘的旋转角速度。 回路电阻为R的电路中(如图16-9所示),求开关K接通长时间后,带电圆盘的旋转角速度。 |
||
 【解】螺线管内离轴线r处的涡旋电场场强 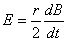 设圆盘的半径为a,在圆盘 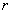 到 到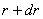 处的 处的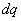 受到的电场力力矩 受到的电场力力矩 式中 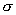 为单位面积上的电荷, 为单位面积上的电荷,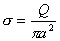 ,圆盘所受的总力矩 ,圆盘所受的总力矩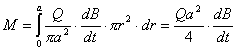 根据转动定律 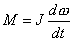 即: 即: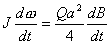 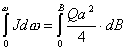 得: 得: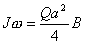 式中 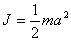 , ,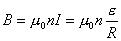 ,代入上式得圆盘最终获得的角速度: ,代入上式得圆盘最终获得的角速度: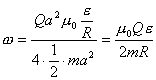 |
||
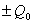 。若在两板中心接一细导线,其电阻R相当大,使电容器缓慢放电,两板上的电荷时时保持均匀。 。若在两板中心接一细导线,其电阻R相当大,使电容器缓慢放电,两板上的电荷时时保持均匀。(1)在图中画出电容器中传导电流和位移电流的分布; (2)试求距中心为r出P点的磁感应强度。 |
||
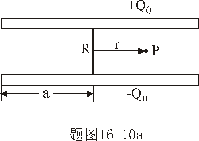 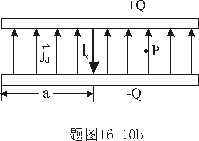 【解】(1)传导电流 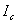 沿中心细导线向下;由于这是电容器放电电路,两极板上的电量随时间减小,随之两极板间场强也随时间减小,即 沿中心细导线向下;由于这是电容器放电电路,两极板上的电量随时间减小,随之两极板间场强也随时间减小,即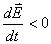 ,所以位移电流密度 ,所以位移电流密度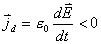 ,与电场强度 ,与电场强度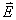 的方向相反,所以 的方向相反,所以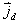 均匀分布且方向向上,如图16-10b所示。 均匀分布且方向向上,如图16-10b所示。(2)RC电容器放电极板上电量随时间的变化规律为: 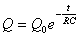 得:  位移电流密度: 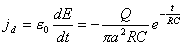 距中心为r处的磁感应强度可根据全电流定理求: 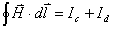 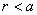 时: 时: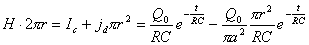 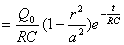 得: 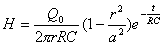 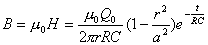 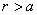 时, 时,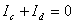
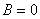 |
||
【答】安培环流定理是可以通过毕-萨定理来证明的。证明过程中应用了稳恒电流闭合的条件,所以安培定理只适用于闭合的载流导线,而对于任意设想的一段载流导线都是不成立的。如果导线不闭合,导线中某瞬时存在电流,则该段导线的两端就会积累正、负电荷,且电量随时间变化,它将引起周围的电场变化,激发起位移电流。由于全电流总是闭合的,对这段导线的全电流考虑,这段导线的安培环流定理总是成立的。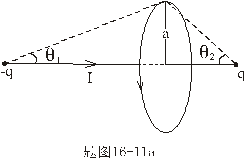 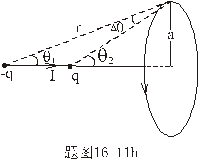 图16-11a所示为一段长直导线,导线内通有传导电流 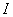 。某瞬间导线两端带有电量 。某瞬间导线两端带有电量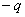 和 和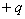 。此时对离导线距离为a的圆环闭合路径所张圆平面的电位移通量(参阅例11-2): 。此时对离导线距离为a的圆环闭合路径所张圆平面的电位移通量(参阅例11-2):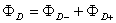 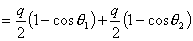 穿过L回路的位移电流: 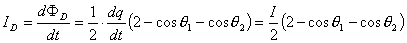 由图16-11a可知,位移电流 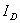 与传导电流I方向相反,全电流: 与传导电流I方向相反,全电流: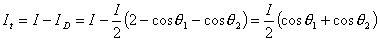 对回路L应用全电流定理: 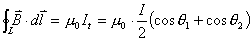 即: 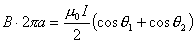 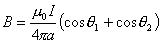 这与毕-萨定理计算的结果一致。 如果闭合回路L所张的圆平面在这段传导电流的延长线方向上,如图b所示,这圆平面的电位移通量: 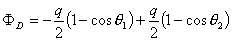 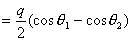 通过这闭合回路L的位移电流: 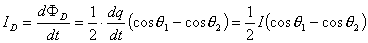 (1) (1)由于传导电流没有与L所张圆平面相交,所以全电流仅为位移电流,对此应用全电流定理:  得: 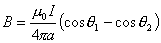 (2) (2)这也与毕-萨定理计算结果相同。 如将图b中的这段电流取得很短为 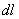 ,则 ,则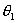 和 和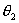 相差很小,用 相差很小,用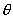 和 和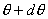 来表示,(1)式中的位移电流可改写如下: 来表示,(1)式中的位移电流可改写如下: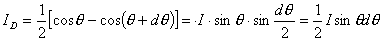 (3)
(3)参考图b的几何关系有: 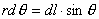 即: 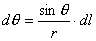 将它代回(3)式,得: 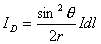 相应于这电流元 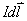 所激发的全电流产生的磁场用 所激发的全电流产生的磁场用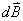 表示,同样对它应用全电流定理: 表示,同样对它应用全电流定理: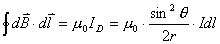 即: 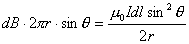 得: 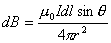 写成矢量形式: 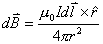 这就通过全电流定理证明了毕-萨定理。也就同时证明了一段电流只从传导电流考虑安培环路定理是不成立的。从全电流考虑,则安培环路定理即全电流定理总是正确的。 |
||
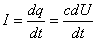
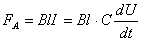 (1)
(1)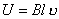 (2)
(2)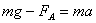 (3)
(3)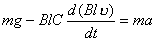
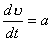 ,上式可化为:
,上式可化为:
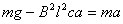
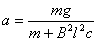
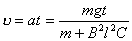
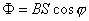 (1)
(1)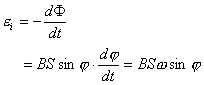 (2)
(2)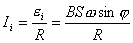 (3)
(3)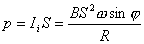
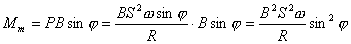
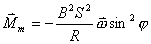
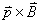 的方向)与
的方向)与