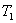 和 和 ,且 ,且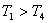 ,当到达热平衡时,求第二和第三块板的热力学温度 ,当到达热平衡时,求第二和第三块板的热力学温度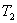 和 和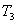 。 。 |
 【解】设各块金属板的面积为S,当第二块板到达热平衡时,满足它左右两面吸收的辐射热和它辐射出去的热量到达平衡: 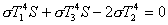 即: 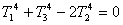 (1) (1)同理对第三块金属板到热平衡时有 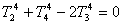 (2) (2)联列(1)(2)式,可求得 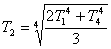 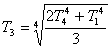 |
(1)对应于最大单色辐出度的辐射波长; (2)在 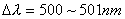 的微小波长范围内,单位时间从小孔辐射出来的能量。 的微小波长范围内,单位时间从小孔辐射出来的能量。 |
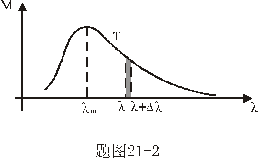 【解】(1)根据维恩位移定律 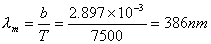 (2)根据普朗克公式 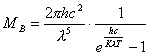 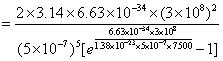  单位时间从小孔辐射出来的波长 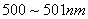 范围内的能量为: 范围内的能量为:  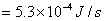 |
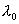 。若以波长为 。若以波长为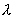 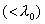 的光照射该金属球,问此金属球至多能发射多少光电子? 的光照射该金属球,问此金属球至多能发射多少光电子? |
【解】因为采用的光波波长 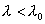 (红限波长),所以能使该金属球产生光电效应。当金属球发射光电子后,金属球就带正电荷,电位就升高,升高到遏止电压 (红限波长),所以能使该金属球产生光电效应。当金属球发射光电子后,金属球就带正电荷,电位就升高,升高到遏止电压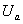 时就不再发射光电子了,由爱因斯坦方程 时就不再发射光电子了,由爱因斯坦方程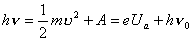 得:  (1) (1)又金属球的电势 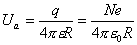 (2) (2)当(1)式等于(2)式时: 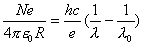 解得金属球能发射的最多电子数: 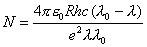 
|
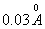 ,测出电子的反冲速度为 ,测出电子的反冲速度为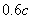 ,求散射光子的波长和散射方向。 ,求散射光子的波长和散射方向。 |
【解】反冲电子所获得的动能 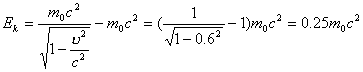 由康普顿散射能量守恒关系 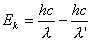 可得: 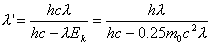 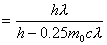 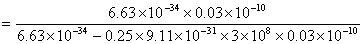 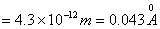 再根据康普顿公式  得: 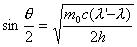  =0.5176 =0.5176得散射光子的方向 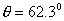 |
【答】光电效应与康普顿效应它们的物理本质是相同的,都不是整个光束与散射物体之间的相互关系,而是个别光子与散射物质内的个别电子之间的相互作用,都不能用光的波动说来解释,都必须用爱因斯坦光子理论作解释。 光电效应与康普顿效应的主要区别是: (1)入射光的波长数量级不同,也就是入射光光子能量的数量级不同。入射光波长为几百埃到几千埃的光子它的能量为几个电子伏特。与电子束缚能同数量级,表现为光电效应。入射光波长小于几埃的 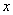 光和 光和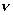 光子,它的能量为几百到几千电子伏特,远大于电子束缚能,此时表现为康普顿效应。 光子,它的能量为几百到几千电子伏特,远大于电子束缚能,此时表现为康普顿效应。(2)光子与电子之间的相互作用表现形式不同。 光电效应中电子吸收光子全部的能量,克服逸出功获得电子的动能,表现为能量守恒。 康普顿效应中,光子与电子碰撞,电子吸收光子的能量,这部分的能量已远大于电子的束缚能。所以可把物质中的外层电子看作为自由电子,同时电子再发射一个散射光子带走一部分能量。所以在康普顿效应中既表现能量守恒,又表现了动量守恒。 |
 。在气体放电管中受到 。在气体放电管中受到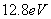 的电子轰击,使氢原子激发,问此放电管中的氢原子从激发态向低能态跃迁时一共能产生几条谱线?其中波长最长的光谱线、最短的光谱线及可见光光谱线的波长各为多少? 的电子轰击,使氢原子激发,问此放电管中的氢原子从激发态向低能态跃迁时一共能产生几条谱线?其中波长最长的光谱线、最短的光谱线及可见光光谱线的波长各为多少? |
【解】基态氢原子受到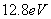 的电子数轰击后,氢原子能具有的最高能量: 的电子数轰击后,氢原子能具有的最高能量: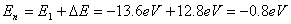 氢原子处于激发态的能量和基态能量的关系为: 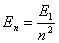 由此,我们可求得氢原子的最大主量子数: 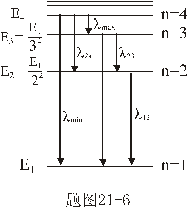
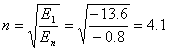 主量子数只能取正整数,所以取4。 在 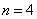 的第三激发态向低能态跃迁一共有主量子数从 的第三激发态向低能态跃迁一共有主量子数从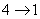 ; ;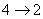 ; ;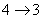 ; ; ; ;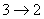 ; ;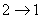 六条谱线。参阅题21-6图。 六条谱线。参阅题21-6图。其中波长最长的为n从 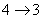 跃迁的光谱线。 跃迁的光谱线。 即 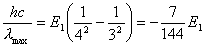  同样,可计算波长最短的为n从 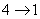 跃迁光谱线: 跃迁光谱线: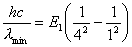 可得 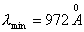 可见光光谱是巴尔麦系,即n由 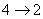 及n由 及n由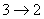 跃迁所得的波长为: 跃迁所得的波长为: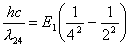 ,可得 ,可得  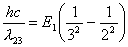 ,可得 ,可得
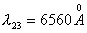 |
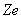 ,核外只剩最后一个电子)轨道半径,电子绕核运动的线速度及原子的能级和电子跃迁时所发射单色光的频率公式。 ,核外只剩最后一个电子)轨道半径,电子绕核运动的线速度及原子的能级和电子跃迁时所发射单色光的频率公式。
|
【解】根据玻尔第三假设电子在稳定轨道运动时它的动量矩满足下式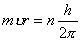 (1) (1)根据牛顿运动定律及库仑定律电子的运动方程  (2) (2)消去(1)式(2)式的 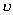 ,并以 ,并以 代替 代替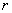 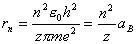 式中 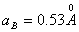 为玻尔半径,将 为玻尔半径,将 代回(1)式可得: 代回(1)式可得: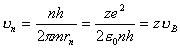 式中 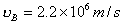 为玻尔轨道上的电子运动速度。原子系统的总能量 为玻尔轨道上的电子运动速度。原子系统的总能量 由(2)式可得  ,代入上式可得 ,代入上式可得 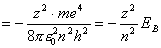 式中 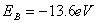 为氢原子基态的能量。 为氢原子基态的能量。按照玻尔第二假设原子系统中电子从较高能级 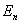 跃迁到较低能级 跃迁到较低能级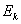 时所发射的单色光频率 时所发射的单色光频率
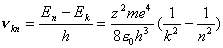  式中R为里德伯恒量 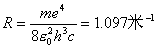 也就是类氢离子的光频在同样n和k能级间跃迁时为氢原子光频 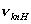 的 的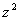 倍。 倍。以二次电离后的 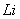 为例,它的 为例,它的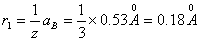 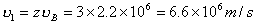 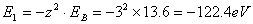 在它的光谱中的最短波长(极限波长)  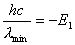 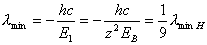  |