势能曲线内容

　　势能曲线是势能随相对位置变化的曲线。它为研究势场中的物体的运动提供了一种形象化的手段。以弹簧振子的势能曲线为例，说明势能曲线的应用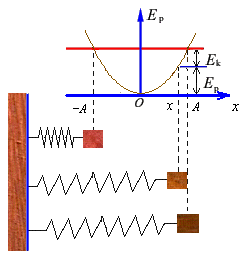

(1)从势能曲线上，可以清晰地看出物体在保守场中运动过程能量的转换关系。 -x 图中，水平线代表系统的总机械能E，势能小于E的区域（-A到A之间）为物体可以到达的相对位置，当物体到达任意位置x时，系统的势能为E_p(见图示），总机械能E与E_p的差值即为该时刻物体的动能E_k。

(2)由势能曲线上各点的斜率大小和正负，可以判定物体所受保守力的大小和方向。

F_x=-

x>0 区间 >0， ∴ F_x<0

x<0 区间 <0， ∴ F_x>0

曲线上斜率大处F_x大，曲线上斜率小处，F_x小，斜率为零处，F_x = 0

(3)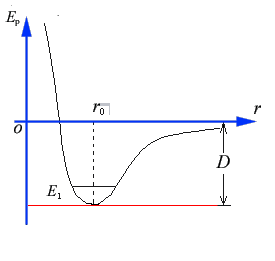 图示为双原子分子的势能曲线，r 是两原子之间的距离。设其中一个原子静止于0点。处曲线斜率为零，两原子相互作用力为零，为分子内两原子间的平衡距离。

当双原子分子系统的总能量E=E₁时，另一原子的运动不会越出势能谷，只能在平衡位置附近振动，这就是稳定的双原子分子的情况。

如果总能量E≥0，则另一原子就能越出势能谷，于是分子离解成两个单独的原子。因此，与势能曲线最低点相应的能量D就称为离解能。

这个势能曲线还可以解释，为什么晶体温度升高时会发生热膨胀现象，温度再升高时，还会发生扩散、熔化等现象。