然而根据光速不变原理,从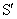 系上观察,则这个事件的时空坐标 系上观察,则这个事件的时空坐标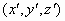 又必定在以 又必定在以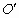 为中心、以 为中心、以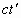 为半径的球面波阵面上,即满足 为半径的球面波阵面上,即满足
现将式(4-2-1)代入式(4-2-3),得
比较式(4-2-4)与式(4-2-2),使它们一致必有
我们还可找出系数之间的另一个关系。取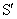 系的原点 系的原点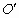 ,由变换关系(4-2-1)可知,它在 ,由变换关系(4-2-1)可知,它在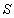 系内的位置必满足 系内的位置必满足
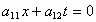
但是,这个 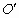 点相对于 点相对于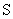 系是以速度 系是以速度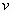 沿 沿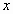 轴运动的,故有 轴运动的,故有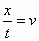 ,因此我们得到 ,因此我们得到
将式(4-2-5)与式(4-2-6)联立,就可以解出系数,即
式(4-2-7)代入式(4-2-1),就得到从 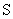 系到 系到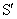 系的变换式: 系的变换式:
由上式解出 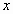 、 、 、 、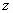 、 、 可得反变换式。用相对性原理可以更简单地导出反变换。因为 可得反变换式。用相对性原理可以更简单地导出反变换。因为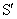 系和 系和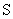 系是等价地,所以从 系是等价地,所以从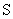 系到 系到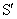 系的变换应该与从 系的变换应该与从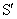 系到 系到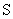 系的变换具有相同形式。若 系的变换具有相同形式。若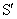 系相对于 系相对于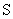 系的运动速度为 系的运动速度为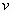 (沿 (沿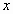 轴正方向),则 轴正方向),则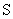 系相对于 系相对于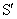 系的速度为 系的速度为 。因此只要把上式中的 。因此只要把上式中的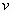 改为 改为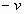 ,把带撇的变量与不带撇的变量相应互换,即得反变换式: ,把带撇的变量与不带撇的变量相应互换,即得反变换式:
|