在一个旋转了的正方体(边长为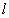 )的无畸变图像中,如果FA边在运动方向上的投影为 )的无畸变图像中,如果FA边在运动方向上的投影为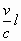 ,则AB边在运动方向上的投影为 ,则AB边在运动方向上的投影为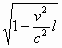 ,可是,现在ABCD面却显示为一个正方形,所以,观察者的眼睛所看到的立方体的图像沿着运动方向膨胀了。由此可见,立方体的图像是畸变了的。 ,可是,现在ABCD面却显示为一个正方形,所以,观察者的眼睛所看到的立方体的图像沿着运动方向膨胀了。由此可见,立方体的图像是畸变了的。
但是,如果我们考虑到相对论效应,则可消除上述图像的畸变,只留下一个不畸变的然而是转过一个角度的该立方体的图像。由于洛仑兹收缩使得AD边和BC边之间的距离减小了(此时正面也成了矩形),变为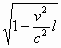 ,同时保持AD边和EF边之间的距离不变。因此,运动立方体的图像就象一个转过一个角度的不畸变的静止立方体的图像。 ,同时保持AD边和EF边之间的距离不变。因此,运动立方体的图像就象一个转过一个角度的不畸变的静止立方体的图像。
需要再次强调的是:上述讨论只有在物体所张的视角很小时才是正确的,只有这样,所看到的图像才是基本上由平行的光信号组成。倘若物体的张角不是很小的话,那么就会导致一些畸变。还有,上述讨论只有当观察者用一只眼睛去看时才是正确的。如果用两只眼睛看,那么由于两眼之间角度的差别,也会使观察者看到畸变。另外,当立方体不高速运动时是看不见的,当它高速运动时就成为可见的了。
从上面的讨论可以看出,对高速运动物体观看时,是看不到洛仑兹收缩的(虽然洛仑兹收缩是客观存在着的)。一旦提到“看见”或“观看”这样的字眼,我们必须即刻意识到这涉及光信号的传播需要一个有限的时间。爱因斯坦在1905年发表了《论动体的电动力学》一文,在这篇著名论文发表之后的50多年以来,物理学家们始终确信一个运动物体的洛仑兹收缩是可以被看见或拍摄下来的,而且一直到1959年以前这个信念从未受到挑战,并且从未受到严密审查。在1959年Terrell证明了观察者是看不到洛仑兹收缩的,并讨论了一些高速运动物体的相对论性外貌的简单而重要的事实。从此,物理学家们才认识到:当我们对光信号从某运动物体的不同部位传到某静止观察者的眼睛所需时间予以适当的考虑时,从该物体的不同部位发出的同时到达视网膜的光信号必定是不同时刻发出的,因此这些发射光信号的不同时刻同整个物体的不同位置有关。这一情况的一般结果是,该物体仿佛发生了畸变。如果运动物体距观察者足够遥远,在后者看来,它所张的立体角很小(以致可近似地认为到达观察者的光线都是彼此平行的),那么该物体看来好像是静止的,并且已旋转了某一角度。这样一些重要的事实竟不被注意达55年之久,一直到Terrell才发现它们,并给予充分的讨论。这些现象在我们研究高速运动物体时有重要意义。在特殊条件下,还可得到有趣的结果,例如乘光子火箭不用绕到某星球的背后就能看到其背面的图像,有兴趣的读者可参看有关文献,例如:Victor Weisskopf, “The Visual Appearance of Rapidly Moving Objects”, Physics Today 13, No.9, 24(1960)。
|