|
研究气体分子速率的分布情况,需要把速率按其大小分成若干相等的间隔。并知道气体在平衡状态下,分布在各个间隔之内的分子数各占气体分子总数的百分数为多少,以及大部分分子的速率分布在哪个间隔之内等等。一句话,就是要知道气体分子的速率分布函数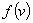 。麦克斯韦经过理论研究,指出在平衡状态中气体分子速率分布函数的具体形式是 。麦克斯韦经过理论研究,指出在平衡状态中气体分子速率分布函数的具体形式是
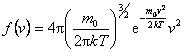
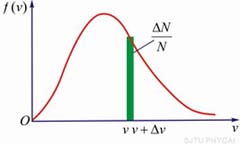
上面的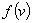 叫做麦克斯韦速率分布函数。表示速率分布函数的曲线叫做麦克斯韦速率分布曲线,如图5-4所示。 叫做麦克斯韦速率分布函数。表示速率分布函数的曲线叫做麦克斯韦速率分布曲线,如图5-4所示。
(a) 某一温度下速率分布曲线 |
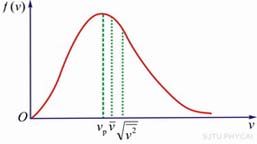
(b) 某一温度下,分子速率的3个统计值 |
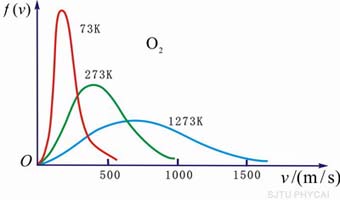 (c)不同温度下的速率分布曲线
图 5-4 麦克斯韦速率分布曲线
(c)不同温度下的速率分布曲线
图 5-4 麦克斯韦速率分布曲线 从图5-4(a)中可以看出,深色的小长方形的面积为
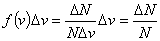
表示某分子的速率在间隔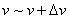 内的概率,也表示在该间隔内的分子数占总分子数的百分数。在不同的向隔内,有不同面积的小长方形,说明不同间隔内的分布百分数不相同。面积较大,表示分子具有该间隔内的速率值的概率也愈大。当 内的概率,也表示在该间隔内的分子数占总分子数的百分数。在不同的向隔内,有不同面积的小长方形,说明不同间隔内的分布百分数不相同。面积较大,表示分子具有该间隔内的速率值的概率也愈大。当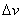 足够微小时,无数矩形的面积总和将渐近于曲线下的面积,这个面积表示分子在整个速率间隔( 足够微小时,无数矩形的面积总和将渐近于曲线下的面积,这个面积表示分子在整个速率间隔(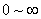 )的概率的总和,按归一化条件,应等于1;即 )的概率的总和,按归一化条件,应等于1;即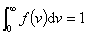 。 。
从速率分布曲线我们还可以知道,具有很大速率或很小速率的分子为数较少,其百分数较低,而具有中等速率的分子为数很多,百分数很高,值得注意的是曲线上有一个最大值,与这个最大值相应的速率值 ,叫做最概然速率。它的物理意义是,在一定温度下,速度大小与 ,叫做最概然速率。它的物理意义是,在一定温度下,速度大小与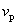 相近的气体分子的百分数为最大,也就是,以相同速率间隔来说,气体分子中速度大小在 相近的气体分子的百分数为最大,也就是,以相同速率间隔来说,气体分子中速度大小在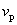 附近的概率为最大。除了方均根速率和最概然速率以外,还有一个有关气体分子速率的平均值——算术平均速率,即分子速率大小的算术平均值(用 附近的概率为最大。除了方均根速率和最概然速率以外,还有一个有关气体分子速率的平均值——算术平均速率,即分子速率大小的算术平均值(用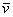 表示),也是十分有用的。图5-4(b)显示出了最概然速率、方均根速率和平均速率。 表示),也是十分有用的。图5-4(b)显示出了最概然速率、方均根速率和平均速率。
不同温度下的分子速率分布曲线,如图5-4(c)所示。当温度升高时,气体分子的速率普遍增大,速率分布曲线上的最大值也向量值增大的方向迁移,亦即最概然速率增大了;但因曲线下的总面积,即分子数的百分数的总和是不变的,因此分布曲线在宽度增大的同时,高度降低,整个曲线将变得“较平坦些”。 |