如果电荷分布已知,那么从点电荷的电场强度公式出发,根据电场强度的叠加原理,就可求出任意电荷分布所激发电场的场强。下面说明计算电场强度的方法
(1) 点电荷的电场强度
设在真空中有一个静止的点电荷q,则距q为r的P点处的电场强度,可由式(7-1)和(7-3)求得。其步骤是先设想在距离点电荷q为r的P点放一试探电荷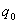 ,由式(7-1)可知,作用在 ,由式(7-1)可知,作用在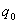 上的电场力是 上的电场力是
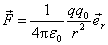
式中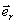 是由点电荷q指向P点的单位矢量,再应用式(7-3)可求得P点的电场强度为 是由点电荷q指向P点的单位矢量,再应用式(7-3)可求得P点的电场强度为
由式(7-6)可知,点电荷q在空间任一点所激发的电场强度大小,与点电荷的电荷量q成正比,与点电荷q到该点距离r的平方成反比。如果q为正电荷,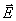 的方向与 的方向与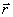 的方向一致,即背离q;如果q为负电荷, 的方向一致,即背离q;如果q为负电荷,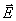 的方向与 的方向与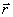 的方向相反,即指向q,如图7-5所示。 的方向相反,即指向q,如图7-5所示。
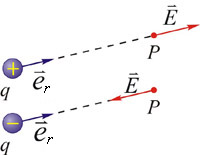 图 7-5 点电荷的电场强度
图 7-5 点电荷的电场强度 |
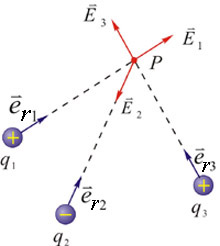 图 7-6 点电荷系的电场强度
图 7-6 点电荷系的电场强度 |
(2) 电场强度叠加原理和点电荷系的电场强度
如果电场是由n个点电荷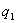 、 、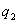 、…、 、…、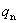 共同激发的,这些电荷组成一个电荷系。根据电场力的叠加原理,试探电荷 共同激发的,这些电荷组成一个电荷系。根据电场力的叠加原理,试探电荷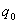 在电荷系的电场中某点P处所受的力等于各个点电荷单独存在时对 在电荷系的电场中某点P处所受的力等于各个点电荷单独存在时对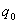 作用的力的矢量和,即 作用的力的矢量和,即
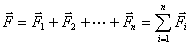
两边除以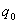 得 得
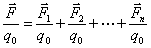
按电场强度的定义,等号右边各项分别是各个点电荷在P点激发的电场强度,而左边为P点的总电场强度,即
上式说明,点电荷系在空间任一点所激发的总电场强度等于各个点电荷单独存在时在该点各自所激发的场强的矢量和。这就是电场强度叠加原理,它是电场的基本性质之一。利用这一原理,可以计算任意带电体所激发的电场强度,因为任何带电体都可以看做许多点电荷的集合。
设各点电荷指向P点的矢量分别为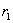 、 、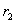 、…、 、…、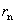 ,按式(7-5),各点电荷在P点处激发的电场强度分别为 ,按式(7-5),各点电荷在P点处激发的电场强度分别为
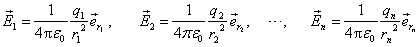
根据场强叠加原理,这个点电荷系在P点所激发的总电场强度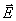 (图7-6)为 (图7-6)为
(3)连续分布电荷的电场强度
从微观结构来看,任何带电体所带的电荷都由大量过剩的电子(或质子)所组成,因而实际上带电体上的电荷分布是不连续的。但从宏观角度出发,可以把电荷看做连续分布在带电体上。一般说来,电荷在带电体上的分布是不均匀的,为了表征电荷在任一点附近的分布情况,我们引入电荷密度的概念。如果电荷分布在整个体积内,这种分布称为体分布。在带电体内任取一点,作一包含该点的体积元ΔV,设该体积中的电荷量为Δq,则该点的电荷体密度ρ定义为Δq与ΔV比值的极限
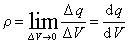
同样地,我们在处理电荷分布在极薄的表面层的问题时,可以把带电薄层抽象为“面带电”,并定义电荷面密度
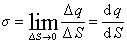
若电荷分布在细长的线上,则定义单位长度所带的电荷为电荷线密度λ
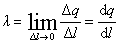
ρ的单位是C/m3,σ的单位为C/m2,λ的单位为C/m。在电荷分布稳定的情况下,ρ,σ和λ都是空间坐标的函数。
应该指出,宏观上看无限小的带电元ΔV、ΔS和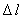 在微观上仍包含大量的基元带电粒子,但引进了连续分布电荷的概念,再应用场强叠加原理,就可以计算任意带电体所激发的电场强度。为此,我们把带电体看做是许多极小的连续分布的电荷元dq的集合,每一个电荷元dq都当作点电荷来处理,而电荷元dq在P点所激发的电场强度,按点电荷的电场强度公式可写为 在微观上仍包含大量的基元带电粒子,但引进了连续分布电荷的概念,再应用场强叠加原理,就可以计算任意带电体所激发的电场强度。为此,我们把带电体看做是许多极小的连续分布的电荷元dq的集合,每一个电荷元dq都当作点电荷来处理,而电荷元dq在P点所激发的电场强度,按点电荷的电场强度公式可写为
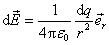
式中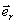 是从dq所在点指向P点的单位矢量。带电体的全部电荷在P点激发的电场强度,是所有的电荷元所激发电场强度 是从dq所在点指向P点的单位矢量。带电体的全部电荷在P点激发的电场强度,是所有的电荷元所激发电场强度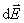 的矢量和,因为电荷是连续分布的,我们把式(7-8)中的累加号Σ换成积分号∫,求得P点的电场强度为 的矢量和,因为电荷是连续分布的,我们把式(7-8)中的累加号Σ换成积分号∫,求得P点的电场强度为
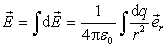
根据带电体上的电荷是体分布、面分布或线分布等不同情况,相应地计算电场强度的式(7-8)可改写为
上三式的右端是矢量的积分式,实际上在具体运算时,通常必须把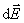 在x、y、z三个坐标轴方向上的分量式写出来,然后再积分。 在x、y、z三个坐标轴方向上的分量式写出来,然后再积分。
由上可见,在求解连续分布电荷的电场强度时大致有这样几个步骤:首先将带电体按其几何形状和带电特征分割成小的带电元dq,并以电荷密度表示;然后写出该带电元dq在所求场点的电场表达式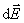 ,分析不同带电元在所求场点的电场方向是否相同,如果不同则必须将矢量式 ,分析不同带电元在所求场点的电场方向是否相同,如果不同则必须将矢量式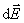 分解,写出 分解,写出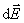 在x、y、z三个坐标轴方向上的分量式,并对这些分量式作积分运算;最后将分量结果合成,得到所论问题的电场强度矢量 在x、y、z三个坐标轴方向上的分量式,并对这些分量式作积分运算;最后将分量结果合成,得到所论问题的电场强度矢量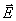 。下面,我们通过几个典型的例题,介绍计算连续分布电荷所激发的电场强度的方法。 。下面,我们通过几个典型的例题,介绍计算连续分布电荷所激发的电场强度的方法。 |