一般情况下,当电荷分布给定时,从高斯定理只能求出通过某一闭合曲面的电场强度通量,并不能把电场中各点的电场强度确定下来。 但是,当电荷分布具有某些特殊的对称性,从而使相应的电场分布也具有一定的对称性时,才有可能应用高斯定理来计算电场强度。所以应用高斯定理求解电场强度时,首先必须对所论问题的电荷分布和电场分布有一个适当的分析,看能不能找出合适的闭合面(习惯上称它为高斯面),使电场强度垂直于这个闭合面,且大小处处相等;或者在闭合面的某一部分上电场强度处处相等且方向与该面垂直,另一部分上电场强度与该面平行,因而通过的电场强度通量为零。 如果能找到这样的闭合面,那么我们就能在应用高斯定理时避免对电场强度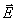 作复杂的积分,而只要计算所作高斯面内的电荷量——这往往是比较容易的。用这样的方法能很方便地求出电场强度。下面举几个简单例子来说明如何应用高斯定理求解电场强度。 作复杂的积分,而只要计算所作高斯面内的电荷量——这往往是比较容易的。用这样的方法能很方便地求出电场强度。下面举几个简单例子来说明如何应用高斯定理求解电场强度。
应用高斯定理求解电场强度要比用式(7-9)计算电场强度简便得多。但这只有当电场具有高度对称性,找得出合适的高斯面时,才有可能应用高斯定理求解电场强度。应该说这个条件是很苛刻的,一般情况下并不能直接用高斯定理来求解电场强度。 |