例题7-3-1 求电荷呈球对称分布时所激发的电场强度。
解:设球半径为R,球所带的电荷量为q。 根据球对称的特点,所激发的电场分布也具有球对称性 不论场点P是在球面外还是在球面内,过P点作半径为r与带电球同心的闭合球面,作为应用高斯定理求解电场强度的高斯面,在这个高斯面上各点电场强度的大小都相等,方向沿径向。
按电荷q均匀分布在球体内和均匀分布在球面上两种情况来讨论。
(1)假定电荷q均匀分布在整个球体内。如果P点在球外,通过高斯面的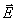 通量为 通量为
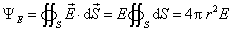
此闭合球面所包围的电荷就是整个球体的电荷量q,因此按照高斯定理有
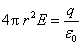
于是 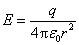
或 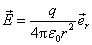
上式与点电荷的电场强度公式完全相同。可见,电荷呈球对称分布时它在球外各点的作用与所带电荷全部集中在球心处的一个点电荷所激发的电场强度一样。
如果P点在球内,同样地,过P点作半径为r与带电球同心的高斯面,那么根据高斯定理,通过高斯面的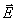 通量为 通量为
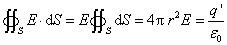
这里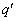 是半径为r(r<R)的高斯面所包围的球体内的电荷量 是半径为r(r<R)的高斯面所包围的球体内的电荷量
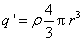
式中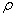 是电荷体密度 是电荷体密度
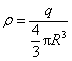
于是得到
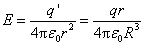
或 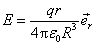
可见球体内部的电场强度随r线性地增加。
(2)若电荷量q均匀分布在半径为R的球面上,又如果P点在球外,按照高斯定理不难推算出球面外的电场强度公式与电荷均匀分布在整个球体内完全相同;但如果P点在球内,则过P点作的高斯面内的电荷量为零,按高斯定理得
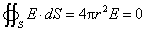
所以 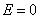
由此可见,均匀带电球面内任何点的电场强度为零。
由上述计算结果,可画出球内、球外各点的电场强度随距离r的变化,如图1和图2所示。从图中可以看出,在球面带电情况下,电场强度E在球面(r=R)附近的值有突变。 在球体带电时,其内部的电场强度随r线性地增加,在球面上达最大值,而且在球面内外两侧的电场强度是连续变化的。
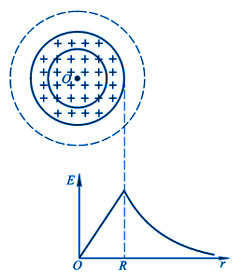 图1 均匀带电球体的电场强度曲线
图1 均匀带电球体的电场强度曲线 |
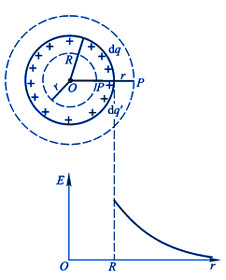 图2 均匀带电球面的电场强度曲线
图2 均匀带电球面的电场强度曲线 |
|