如前所述,如果把激发外电场的原有电荷系称为自由电荷,并用 表示它们所激发的电场强度,而用 表示它们所激发的电场强度,而用 表示极化过程完成之后极化电荷所激发的电场强度。那么,空间任一点最终的合电场强度 表示极化过程完成之后极化电荷所激发的电场强度。那么,空间任一点最终的合电场强度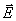 应是上述两类电荷所激发电场强度的矢量和,即 应是上述两类电荷所激发电场强度的矢量和,即
由于在电介质中,自由电荷的电场与极化电荷的电场的方向总是相反,所以在电介质中的合电场强度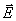 与外电场强度 与外电场强度 相比显著地削弱了。 相比显著地削弱了。
对于大多数常见的电介质,电极化强度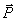 与作用于介质内部的合电场强度 与作用于介质内部的合电场强度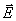 成正比,而且两者方向相同,在国际单位制中可表示为
式中的比例系数 成正比,而且两者方向相同,在国际单位制中可表示为
式中的比例系数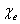 和电介质的性质有关,叫做介质的电极化率,是量纲为1的量。服从式(7-56)极化规律的电介质叫做各向同性的线性电介质。 和电介质的性质有关,叫做介质的电极化率,是量纲为1的量。服从式(7-56)极化规律的电介质叫做各向同性的线性电介质。
为了定量地了解电介质内部电场强度被削弱的情况,我们讨论如下特例。图7-38表示在两块“无限大”极板间充有极化率为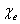 的均匀电介质,设两极板上的自由电荷面密度为 的均匀电介质,设两极板上的自由电荷面密度为 ,电介质表面上的极化电荷面密度为 ,电介质表面上的极化电荷面密度为 。自由电荷的电场强度大小 。自由电荷的电场强度大小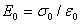 , 在图中用实线表示; 极化电荷的电场强度大小 , 在图中用实线表示; 极化电荷的电场强度大小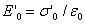 ,在图中用虚线表示。 ,在图中用虚线表示。  的方向和 的方向和 的方向相反,因此极板间电介质中的合电场强度 的方向相反,因此极板间电介质中的合电场强度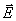 的大小为
考虑到极化电荷面密度为 的大小为
考虑到极化电荷面密度为 ,以及式(7-61),极板间电介质中的合电场强度 ,以及式(7-61),极板间电介质中的合电场强度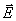 的大小又可写为 的大小又可写为
说明电介质内部的电场强度E被削弱为外电场强度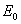 的 的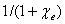 。下面我们将看到 。下面我们将看到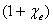 正是电介质的相对电容率 正是电介质的相对电容率 。两极板间的电势差为 。两极板间的电势差为
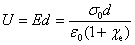
设极板的面积为S,则极板上总的电荷量为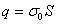 ,按电容器电容的定义,当极板间充满均匀电介质后的电容为 ,按电容器电容的定义,当极板间充满均匀电介质后的电容为
与式(7-47)比较,可得
这就解释了电容器中充满电介质后其电容增大的实验事实。又令
称作电介质的电容率或介电常量,与真空中的电容率 有相同的单位。 极化率 有相同的单位。 极化率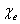 、相对电容率 、相对电容率 和电容率 和电容率 都是表征电介质性质的物理量,三者中知道任何一个即可求得其他两个。式(7-60)和式(7-61)虽然是从平行板电容器中均匀电介质的特例引出的,但它们却是普遍适用的。 都是表征电介质性质的物理量,三者中知道任何一个即可求得其他两个。式(7-60)和式(7-61)虽然是从平行板电容器中均匀电介质的特例引出的,但它们却是普遍适用的。
应该指出,(7-58)式表明,在均匀电介质充满整个电场的情况下,电介质内部的电场强度E为电场强度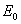 的 的 倍,这一结论并不是普遍成立的,但电介质内部的电场强度通常要减弱,这个现象却是普遍成立的。 倍,这一结论并不是普遍成立的,但电介质内部的电场强度通常要减弱,这个现象却是普遍成立的。
最后还必须指出,无论是自由电荷还是极化电荷,从激发电场的角度看,它们所激发的静电场特性应是一样的。所以有电介质存在时,电场强度的环路定理仍然成立,即

式中的E 是所有电荷(自由电荷和极化电荷)所激发的静电场中各点的合电场强度。
|






