1.毕奥–萨伐尔定律
这部分我们讨论一下由恒定电流所激发的磁场。如图8-11所示,设真空中有电流为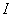 的任意形状的载流导线, 的任意形状的载流导线,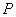 为任意场点。导线与场点的距离较导线直径大得多,这种电流称为线电流。那么如何求这段载流导线在 为任意场点。导线与场点的距离较导线直径大得多,这种电流称为线电流。那么如何求这段载流导线在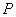 点产生的磁感应强度呢?回想如何计算任意形状的带电体在其周围产生电场的计算问题:先把 点产生的磁感应强度呢?回想如何计算任意形状的带电体在其周围产生电场的计算问题:先把
带电体分割成许多电荷元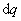 ,根据库仑定律,电荷元所激发的场强 ,根据库仑定律,电荷元所激发的场强
再应用叠加原理,便可得出任意带电体在空间各点形成的场强。
|
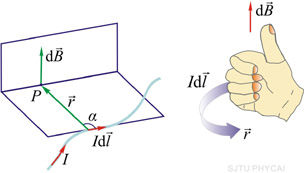 图 8-11
图 8-11
|
与此相似,为求电流所激发的磁场,我们也可以把电流看做是无穷多小段电流的集合。各小段电流称为电流元,并用矢量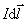 来表示, 来表示,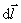 表示在载流导线上(沿电流方向)所取的线元, 表示在载流导线上(沿电流方向)所取的线元, 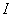 为导线中的电流强度。任意形状的线电流所激发的磁场等于各段电流元所激发磁场的矢量和。拉普拉斯在研究和分析了毕奥、萨伐尔等人的实验资料后,找出了电流元 为导线中的电流强度。任意形状的线电流所激发的磁场等于各段电流元所激发磁场的矢量和。拉普拉斯在研究和分析了毕奥、萨伐尔等人的实验资料后,找出了电流元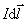 在空间任一点 在空间任一点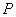 处所激发的磁感应强度 处所激发的磁感应强度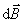 的大小为 的大小为
式中的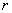 是从电流元所在点到 是从电流元所在点到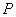 点的矢量 点的矢量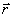 的大小, 的大小, 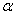 为 为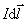 与 与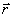 之间小于 之间小于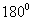 的夹角。 的夹角。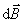 的方向垂直于 的方向垂直于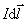 与 与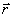 组成的平面,指向为由 组成的平面,指向为由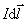 一经 一经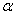 角转向 角转向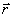 时右螺旋前进的方向,如图8-11所示。在国际单位制中, 时右螺旋前进的方向,如图8-11所示。在国际单位制中,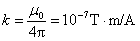 ; ;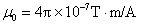
称为真空磁导率。把上写成矢量式为
称为毕奥–萨伐尔定律,是计算电流磁场的基本公式。任意线电流所激发的总磁感应强度为
2.运动电荷的磁场
一切磁现象都起源于电荷的运动,下面将从毕奥–萨伐尔定律出发导出运动电荷的磁场表达式。 设在导体的单位体积内有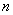 个可以作自由运动的带电粒子,每个粒子带有电荷量 个可以作自由运动的带电粒子,每个粒子带有电荷量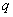 以速度 以速度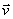 运动而形成导体中的电流。如果电流元的截面为 运动而形成导体中的电流。如果电流元的截面为 ,那么通过截面 ,那么通过截面 的电流 的电流 为 为
在电流元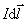 内有 内有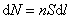 个带电粒子以速度 个带电粒子以速度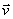 运动着, 运动着,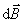 就是这些运动电荷所激发的磁场,将 就是这些运动电荷所激发的磁场,将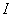 代人毕奥–萨伐尔定律,我们就可度得到每一个以速度 代人毕奥–萨伐尔定律,我们就可度得到每一个以速度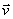 运动的电荷所激发的磁感应强度为 运动的电荷所激发的磁感应强度为
3.毕奥-萨伐尔定律的应用
根据毕奥-萨伐尔定律,原则上讲,我们可以计算任何稳恒电流系统所产生的磁场。
在应用毕奥-萨伐尔定律求解载流导体的磁感应强度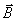 时,首先必须将载流导体分割成无限个电流元I 时,首先必须将载流导体分割成无限个电流元I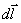 ,按式(8-21)写出电流元I ,按式(8-21)写出电流元I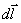 在所求点的磁感应强度 在所求点的磁感应强度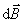 ,然后按照式(8-22)的磁感应强度 ,然后按照式(8-22)的磁感应强度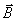 叠加原理求出所有电流元在该点的磁感应强度的矢量和。由于式(8-22)是一矢量积分,各电流元在所求点的磁感应强度 叠加原理求出所有电流元在该点的磁感应强度的矢量和。由于式(8-22)是一矢量积分,各电流元在所求点的磁感应强度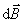 的方向可能不同,所以我们还必须按所选取的坐标将 的方向可能不同,所以我们还必须按所选取的坐标将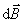 作一分解,例如在直角坐标系中可将 作一分解,例如在直角坐标系中可将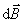 分解为 分解为
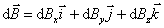
然后对各分量进行积分
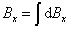 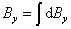 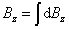
最后得到所求点的磁感应强度
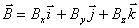
下面应用毕奥-萨伐尔定律来求解一些常用的载流导体的磁感应强度。
(1)载流长直导线的磁场
设有长为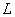 的载流直导线,其中电流为 的载流直导线,其中电流为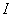 ,如图8-13所示。计算离直导线距离为 ,如图8-13所示。计算离直导线距离为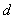 的 的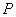 点的磁感应强度时,首先在直导线上任取一电流元 点的磁感应强度时,首先在直导线上任取一电流元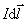 ,按毕奥-萨伐尔定律,这电流元在给定点的磁感应强度为 ,按毕奥-萨伐尔定律,这电流元在给定点的磁感应强度为
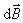 的方向由 的方向由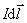 来确定,即垂直纸面向内,由于长直导线 来确定,即垂直纸面向内,由于长直导线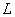 上每一个电流元在 上每一个电流元在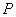 点的磁感应强度 点的磁感应强度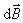
在实际问题中,如直导线的长度远远大于从导线到场点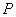 的距离,就能近似应用上述公式。 的距离,就能近似应用上述公式。
(2)载流圆线圈轴线上的磁场
设有单匝载流圆线圈(也称圆电流),其半径为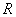 ,通以电流 ,通以电流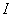 ,如图8-14所示。计算载流圆线圈 ,如图8-14所示。计算载流圆线圈
各电流元在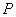 点的磁感应强度大小相等,方向各不相同,但各 点的磁感应强度大小相等,方向各不相同,但各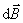 与轴线成一相等的夹角.我们把 与轴线成一相等的夹角.我们把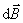 分解为平行于轴线的分矢 分解为平行于轴线的分矢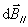 衡与垂直于轴线的分矢量 衡与垂直于轴线的分矢量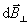 。由于对称关系,任一直径两端的电流元在 。由于对称关系,任一直径两端的电流元在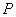 点的磁感应强度的垂直轴线的分量 点的磁感应强度的垂直轴线的分量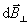 大小相等,方向相反,因此,载流圆线圈上电流在 大小相等,方向相反,因此,载流圆线圈上电流在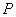 点 点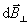 互相抵消,而 互相抵消,而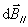 互相加强。所以 互相加强。所以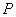 点磁感应强度为圆形线圈上所有电流元的 点磁感应强度为圆形线圈上所有电流元的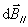 的代数和,即 的代数和,即
式中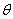 为 为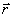 与轴线的夹角。将 与轴线的夹角。将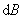 带入得 带入得
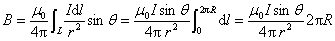
利用 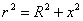 , , 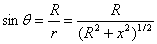
最终有
式中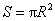 为圆线圈的面积。 为圆线圈的面积。
圆线圈轴线上各点的磁感应强度都沿轴线方向,与电流方向组成右手螺旋关系,离圆心距离 越远,磁场越弱。 越远,磁场越弱。
下面讨论两个特殊点处的情况:
在圈心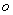 点处, 点处,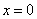 ,由上式得 ,由上式得
在远离线圈处,即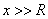 , ,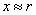 则轴线上各点的 则轴线上各点的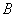 值近似为 值近似为 |
|
令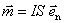 ,将磁感应强度写成矢量式 ,将磁感应强度写成矢量式
此式和电偶极子在轴线上场强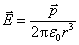 相似,所以我们把 相似,所以我们把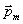 称为载流线圈的磁矩,它的大小等于 称为载流线圈的磁矩,它的大小等于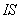 ,它的方向与线圈平面的法线方向相同且与电流呈右螺旋关系。式中的 ,它的方向与线圈平面的法线方向相同且与电流呈右螺旋关系。式中的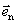 表示法线方向的单位矢量。如果线圈有 表示法线方向的单位矢量。如果线圈有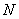 匝,则磁场加强 匝,则磁场加强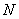 倍,这时线圈磁矩要定义为 倍,这时线圈磁矩要定义为
(3)载流直螺线管内部的磁场
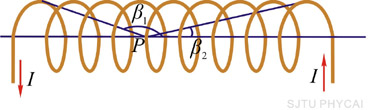
均匀密绕在直圆柱面上的一螺旋形线圈称为直螺线管,如图8-15(a)所示。设螺线管的半径为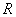 ,电流为 ,电流为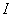 ,每单位长度有线圈 ,每单位长度有线圈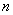 匝。计算载流直螺线管内部轴线上的磁场时, 匝。计算载流直螺线管内部轴线上的磁场时,
(a) |
(b) |
图 8-15 |
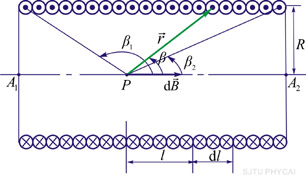
首先在螺线管上任取一小段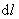 ,这小段上有线圈 ,这小段上有线圈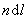 匝。由于管上线圈绕得很紧密,这小段上的线圈相当于电流为 匝。由于管上线圈绕得很紧密,这小段上的线圈相当于电流为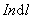 的一个圆形电流。应用载流圆线圈轴线上的磁场公式,可知这小段上的线圈在轴线上某点 的一个圆形电流。应用载流圆线圈轴线上的磁场公式,可知这小段上的线圈在轴线上某点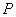 所激发的磁感应强度 所激发的磁感应强度
式中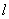 是 是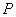 点到螺线管上 点到螺线管上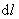 处这一小段线圈的长度,磁感应强度的方向沿轴线向右。因为螺线管的各小段在 处这一小段线圈的长度,磁感应强度的方向沿轴线向右。因为螺线管的各小段在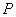 点所产生的磁感应强度的方向都相同,矢量积分化为标量积分,因此整个螺线管所产生的总磁感应强度 点所产生的磁感应强度的方向都相同,矢量积分化为标量积分,因此整个螺线管所产生的总磁感应强度
为了便于积分,我们引人新变量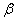 角,也就是螺线管的轴线与从 角,也就是螺线管的轴线与从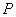 点到 点到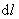 处小段线圈上任一点的矢量 处小段线圈上任一点的矢量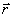 之间的夹角。于是有关系(图8-15(b)) 之间的夹角。于是有关系(图8-15(b))
微分上式得
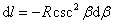 ,又 ,又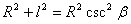
将以上关系式及积分变量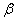 的上下限 的上下限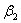 和 和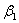 代人式(8-37)后得 代人式(8-37)后得
如果螺线管为“无限长”,亦即螺线管的长度较其直径大得多时,显然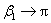 , ,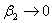
这一结果说明:任何绕得很紧密的长螺线管内部轴线上的磁感应强度和点的位置无关。还可以证明,对于不在轴线上的内部各点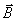 的值也等于 的值也等于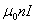 ,因此“无限长”螺线管内部的磁场是均匀的,可以利用螺线管的这一性质来产生匀强磁场。 ,因此“无限长”螺线管内部的磁场是均匀的,可以利用螺线管的这一性质来产生匀强磁场。
对长螺线管的端点来说,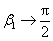 , ,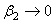 该点处的磁感应强度为 该点处的磁感应强度为
恰好是内部磁感应强度的一半。长直螺线管所激发的磁感应强度的方向沿着螺线管轴线,其指向可按右手定则确定,右手四指表示电流的流向,拇指就是磁场的指向。轴线上各处磁感应强度的量值变化情如图8-16所示。
|
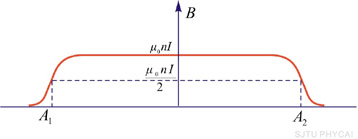
图 8-16 |
|






