1.安培定律
实验指出,放置在磁场中的载流导线要受到磁场力的作用,这个力叫做安培力,产生安培力的微观机制如下。
我们在载流导线上任取一电流元,该电流元所在处的磁感应强度为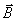 (图8-35)。设导线中每个自由电子以平均速度向右作定向运动,则每个自由电子受到洛伦兹力 (图8-35)。设导线中每个自由电子以平均速度向右作定向运动,则每个自由电子受到洛伦兹力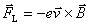 的作用,电子通过与材料晶格的不断碰撞,把这个力传给了电流元,这样整个电流元在磁场中所受的安培力 的作用,电子通过与材料晶格的不断碰撞,把这个力传给了电流元,这样整个电流元在磁场中所受的安培力
|
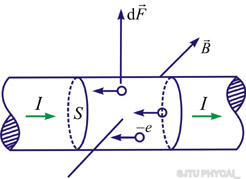
图 8-35 |
式中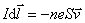 ,注意,自由电子定向运动的方向与电流元的方向相反。顺便指出,在上述推导过程中,我们没有考虑载流导线自身激发的磁场,事实上,载流导线不可能产生作用在导线自身上的力。 ,注意,自由电子定向运动的方向与电流元的方向相反。顺便指出,在上述推导过程中,我们没有考虑载流导线自身激发的磁场,事实上,载流导线不可能产生作用在导线自身上的力。
上式称为安培定律,是安培首先由实验总结出来的基本规律。
根据安培力公式,原则上讲,一段任意形状的载流导线所受的磁场力问题已经解决,即
2.磁场对载流线圈的作用
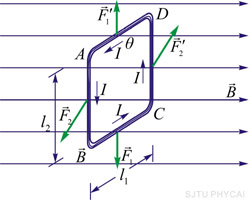
如图8-36所示,在磁感应强度为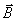 的匀强磁场中,有一刚性的长方形平面载流线圈,边长分别为 的匀强磁场中,有一刚性的长方形平面载流线圈,边长分别为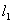 和 和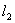 ,电流为 ,电流为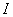 ,设线圈的平面与磁场的方向成任意角 ,设线圈的平面与磁场的方向成任意角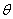 ;对边 ;对边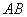 、 、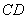 与磁场垂直,根据安培定律,导线 与磁场垂直,根据安培定律,导线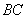 和 和 所受的磁场力分别为 所受的磁场力分别为
(a) |
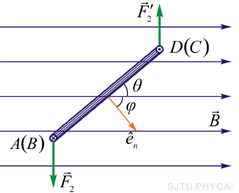
(b) |
图 8-36 |
这两个力在同一直线上,大小相等而方向相反,相互抵消。导线 和 和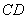 所受的磁场力分别为 所受的磁场力分别为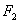 和 和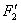 , ,
这两个力大小相等,指向相反,但力的作用线不在同一直线上,因此形成一力偶,力臂为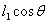 。它们作用在线圈上的力偶矩为 。它们作用在线圈上的力偶矩为
式中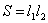 为线圈的面积。 为线圈的面积。
如果用线圈平面的正法线方向和磁场方向的夹角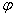 来代替 来代替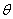 ,由于 ,由于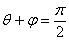 ,所以上式应为 ,所以上式应为
如果线圈有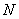 匝,那么线圈所受的力偶矩为 匝,那么线圈所受的力偶矩为
上式中的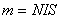 ;是线圈的磁矩,磁矩是矢量,用 ;是线圈的磁矩,磁矩是矢量,用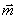 表示,磁矩的方向就是载流线圈平面法线的正方向,所以式(8-97)也可写成矢量式 表示,磁矩的方向就是载流线圈平面法线的正方向,所以式(8-97)也可写成矢量式
应用磁力矩公式时, 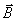 的单位用 的单位用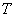 , ,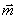 的单位用 的单位用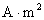 ,力矩的单位用 ,力矩的单位用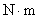 。 。
平面载流线圈在均匀磁场中任意位置上所受的合力均为零,仅受力矩的作用。因此在均匀磁场中的平面载流线圈只发生转动,不会发生整个线圈的平动。磁场对载流线圈作用力矩的规律是制成各种电动机、动圈式电表和电流计等的基本原理。
当电流通过线圈时,线圈在磁场中受到磁力矩的作用而转动。由于磁场是径向均匀的,所以无论线圈转到什么位置,线圈平面的法线方向总是和线圈所在处的磁场方向垂直,因此,线圈所受的磁力矩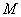 的大小是不变的,即 的大小是不变的,即
当线圈转动时,游丝就要被卷紧,卷紧的游丝给线圈一个反方向的扭转力矩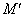 。根据实验测定,游丝给线圈的扭转力矩与线圈转过的角度 。根据实验测定,游丝给线圈的扭转力矩与线圈转过的角度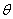 成正比,即 成正比,即
式中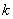 称为游丝的扭转常量,对于一定的游丝来说 称为游丝的扭转常量,对于一定的游丝来说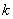 是常量。 是常量。
当线圈受到的磁力矩和游丝给线圈的扭转力矩相互平衡时,线圈就稳定在这个位置,这时
所以
式中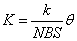 是恒量,通常称为电流计常量。它表示电流计偏转单位角度时所需通过的电流。 是恒量,通常称为电流计常量。它表示电流计偏转单位角度时所需通过的电流。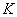 值越小,电流计越灵敏。因此,线圈偏转的角度 值越小,电流计越灵敏。因此,线圈偏转的角度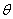 与通过线圈的电流 与通过线圈的电流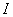 成正比关系,这样就可以从指针所指的位置来测量电流,这就是磁电式电流计的工作原理。 成正比关系,这样就可以从指针所指的位置来测量电流,这就是磁电式电流计的工作原理。
3.平行载流导线间的相互作用力 电流单位“安培”的定义
毕奥—萨伐尔定律描述电流元所激发的磁场,安培定律描述电流元在磁场中所受的磁场力,根据这两个定律,原则上可以计算任意形状的载流导线之间或载流线圈之间的相互作用。
计算载流导线所受磁场力的步骤是:首先计算导线上任一电流元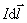 所受的力 所受的力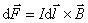 ,式中 ,式中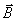 为其他载流导线在 为其他载流导线在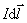 所在处所激发的总磁感应强度, 所在处所激发的总磁感应强度,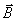 需要按毕奥–萨伐尔定律来计算;其次用积分法再求整个载流导线上各个电流元所受的力的矢量和。 需要按毕奥–萨伐尔定律来计算;其次用积分法再求整个载流导线上各个电流元所受的力的矢量和。
下面我们按上述步骤计算两条“无限长”的平行载流直导线之间的相互作用力。
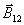 的方向如图所示,垂直于电流元 的方向如图所示,垂直于电流元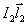 ,所以 ,所以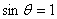 ,因而 ,因而
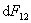 的方向在两平行载流直导线所决定的平面内,指向导线 的方向在两平行载流直导线所决定的平面内,指向导线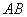 。 。
显然,载流导线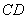 上各个电一流元所受的力方向都与上述方向相同,所以导线 上各个电一流元所受的力方向都与上述方向相同,所以导线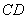 单位长度所受的力为 单位长度所受的力为
同理可以证明载流导线AB单位长度所受的力的大小也等于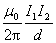 ,方向指向导线 ,方向指向导线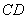 :这就是说,两个同方向的平行载流直导线,通过磁场的作用,将互相吸引。不难看出,两个反向的平行载流直导线,通过磁场的作一用,将互相排斥,而每一导线单位长度所受的斥力的大小与这两电流同方向时的引力相等。 :这就是说,两个同方向的平行载流直导线,通过磁场的作用,将互相吸引。不难看出,两个反向的平行载流直导线,通过磁场的作一用,将互相排斥,而每一导线单位长度所受的斥力的大小与这两电流同方向时的引力相等。
由于电流比电荷量更容易测定,在国际单位制中把安培定为基本单位。安培的定义如下:真空中相距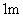 的二无限长而圆截面极小的平行直导线中载有相等的电流时,若在每米长度导线上的相互作用力正好等于 的二无限长而圆截面极小的平行直导线中载有相等的电流时,若在每米长度导线上的相互作用力正好等于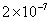 N,则导线中的电流定义为 N,则导线中的电流定义为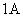 。 。
在国际单位制中,真空磁导率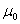 是导出量。根据安培的定律,上式中 是导出量。根据安培的定律,上式中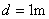 , ,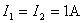 , ,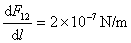 ,从而可得 ,从而可得
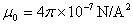
4.磁场力的功
载流导线或载流线圈在磁场内受到磁场力(安培力)或磁力矩的作用,因此,当导线或圈的位置与方位改变时,磁场力就作了功。下面从一些特殊情况出发,建立磁场力作功的一般公式。
在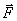 力的作用下, 力的作用下,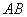 将从初始位置沿着 将从初始位置沿着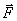 力的方向移动,当移动到位置 力的方向移动,当移动到位置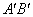 时磁场力 时磁场力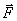 所作的功 所作的功
当导线在初始位置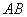 和在终了位置 和在终了位置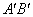 时,通过回路的磁通量分别为 时,通过回路的磁通量分别为
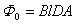 , 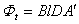 |
(8-109) |
所以磁通量的增量为
可知在导线移动中,磁场力所作的功为
式中的负号表示磁力矩作正功时将使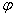 减小。因为 减小。因为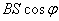 表示通过线圈的磁通量,故 表示通过线圈的磁通量,故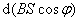 就表示线圈转过后 就表示线圈转过后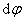 磁通量的增量 磁通量的增量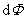 。所以上式也可写成 。所以上式也可写成
当上述载流线圈从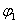 转到 转到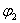 时,按上式积分后得磁力矩所作的总功 时,按上式积分后得磁力矩所作的总功
式中的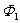 和 和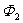 ,分别表示线圈在 ,分别表示线圈在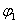 和 和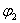 时通过线圈的磁通量。 时通过线圈的磁通量。
可以证明,一个任意的闭合电流回路在磁场中改变位置或形状时,如果保持回路中电流不变,则磁场力或磁力矩所作的功都可按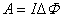 计算,亦即磁场力或磁力矩所作的功等于电流乘以通过载流线圈的磁通量的增量,这是磁场力作功的一般表示。 计算,亦即磁场力或磁力矩所作的功等于电流乘以通过载流线圈的磁通量的增量,这是磁场力作功的一般表示。
|






