1.在磁场中运动的导线内的感应电动势
这里,通过回路面积磁通量的增量也就是导线在运动过程中所切割的磁感应线数,所以以动生电动势在量值上等于在单位时间内导线所切割的磁感应线数。
由式中的负号或楞次定律,可以确定动生电动势的方向是从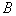 指向 指向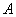 的。这时要注意,电动势是导线运动产生的,这个电动势只存在于导线 的。这时要注意,电动势是导线运动产生的,这个电动势只存在于导线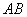 段内,即运动着的导线 段内,即运动着的导线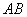 相当于一个电源,在电源内部,电动势方向是由低电势指向高电势的。因此 相当于一个电源,在电源内部,电动势方向是由低电势指向高电势的。因此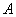 点的电势比 点的电势比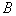 点的高。这就是说, 点的高。这就是说,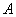 端相当于电源的正极, 端相当于电源的正极,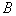 端相当于负极,这同用右手法则来确定动生电动势的方向所得出的结果是一致的。 端相当于负极,这同用右手法则来确定动生电动势的方向所得出的结果是一致的。
2.动生电动势的微观解释
导体在磁场中运动切割磁感应线而产生的电动势,可用金属电子理论来解释,式(9-6)可以从理论上导出。当导线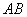 以速度 以速度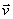 向右运动时,导线内每个自由电子也就获得向右的定向速度,由于导线处在磁场中,自由电子受到的洛伦兹力 向右运动时,导线内每个自由电子也就获得向右的定向速度,由于导线处在磁场中,自由电子受到的洛伦兹力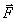 为 为
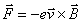
式中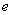 为电子电荷量的绝对值。 为电子电荷量的绝对值。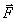 的方向沿导线从 的方向沿导线从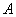 指向 指向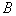 ,电子在力 ,电子在力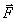 作用下,将沿导线从 作用下,将沿导线从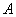 端向 端向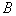 端运动,结果在回路中出现逆时针方向的感应电流。非静电力就是洛伦兹力 端运动,结果在回路中出现逆时针方向的感应电流。非静电力就是洛伦兹力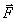 ,它可以看做等效于一个非静电性场强对电子的作用,即 ,它可以看做等效于一个非静电性场强对电子的作用,即
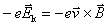
或
由于回路的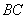 、 、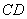 和 和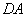 段相对磁场静止,其中非静电性场强 段相对磁场静止,其中非静电性场强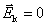 ,只有 ,只有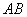 段中的 段中的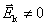 ,由矢量积关系可知, ,由矢量积关系可知,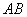 段中的 段中的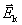 平行于 平行于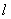 ,所以在回路 ,所以在回路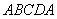 中的感应电动势 中的感应电动势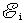 为 为
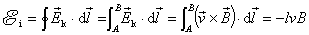
这结果与式(9-6)完全一致。这表明形成动生电动势的实质是运动电荷受洛伦兹力的结果。
在一般情况下,磁场可以不均匀,导线在磁场中运动时各部分的速度也可以不同,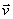 、 、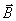 和 和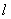 也可以不相互垂直,这时运动导线内总的动生电动势可用式 也可以不相互垂直,这时运动导线内总的动生电动势可用式
来计算。这里线元矢量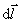 的方向是任意选定的,当 的方向是任意选定的,当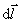 与 与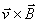 间呈锐角时, 间呈锐角时,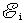 为正,表示 为正,表示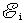 顺着 顺着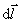 方向;呈钝角时, 方向;呈钝角时,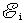 为负,表示 为负,表示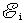 逆着方向。 逆着方向。
在回路中(图9-7)建立起感应电流后,载流导线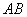 段在外磁场中又要受到安培力 段在外磁场中又要受到安培力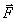 的作用,其大小为 的作用,其大小为
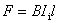
方向在纸面内垂直于导线向左(图9-8)。所以,如要维持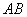 向右作匀速运动,使在 向右作匀速运动,使在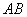 段导线中产生恒定的电动势,从而在回路中建立起恒定的感应电流 段导线中产生恒定的电动势,从而在回路中建立起恒定的感应电流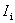 ,就必须在 ,就必须在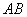 段上施加一同样大小方向向右的外力 段上施加一同样大小方向向右的外力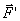 (回路的另外三段边框固定,受力情况不讨论)。自此,在维持段 (回路的另外三段边框固定,受力情况不讨论)。自此,在维持段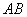 导线作匀速运动过程中,外力 导线作匀速运动过程中,外力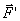 必须克服安培力 必须克服安培力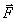 而作功,它所消耗的恒定功率为 而作功,它所消耗的恒定功率为
实质上,我们这里所讨论的就是发电机的工作原理,也就是动生电动势的一个实际应用。发电机是把机械能转化为电能的装置,从力学方面来说,外力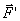 作功表示外界向发电机供给了机械能,磁场力 作功表示外界向发电机供给了机械能,磁场力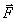 作负功表示发电机接受了此能量,在电路方面来说,电源(即“运动导线 作负功表示发电机接受了此能量,在电路方面来说,电源(即“运动导线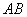 ”)的电动势为 ”)的电动势为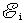 ,电源向电路中供应出电能,其电功率为 ,电源向电路中供应出电能,其电功率为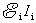 。由此可见,“磁场力 。由此可见,“磁场力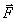 作负功,接受了机械能”和“电源向电路中供应出电能”就是“机械能向电能转化”同一事实的两个侧面。所以,要使发电机不断地工作,就得用水轮机、汽轮机或其他动力机械带动导线运动,把机械能不断地转化为电能。 作负功,接受了机械能”和“电源向电路中供应出电能”就是“机械能向电能转化”同一事实的两个侧面。所以,要使发电机不断地工作,就得用水轮机、汽轮机或其他动力机械带动导线运动,把机械能不断地转化为电能。
3.在磁场中转动的线圈内的感应电动势
这里我们讨论一个在均匀磁场中作匀速转动的矩形线圈。设矩形线圈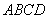 的匝数为 的匝数为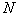 ,面积为 ,面积为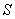 ,使这个线圈在匀强磁场中绕固定的轴线 ,使这个线圈在匀强磁场中绕固定的轴线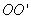 转动,磁感应强度 转动,磁感应强度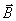 与 与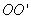 轴垂直(图9-9)。当 轴垂直(图9-9)。当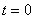 时,线圈平面的法线单位矢量 时,线圈平面的法线单位矢量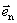 与磁感应强度 与磁感应强度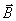 之间的夹角为零,经过时间 之间的夹角为零,经过时间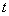 ,线圈平面的法线单位矢量之夹角 ,线圈平面的法线单位矢量之夹角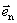 与 与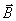 之夹角为 之夹角为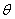 ,这时通过每匝线圈平面的磁通量为 ,这时通过每匝线圈平面的磁通量为
式(9-9)也可用洛伦兹力的观点导出。当线圈平面法线单位矢量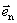 与 与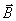 之夹角为 之夹角为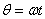 时, 时,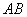 段上各点都以速度 段上各点都以速度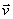 运动,按式(9-7), 运动,按式(9-7),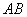 段中的等效非静电性场强为 段中的等效非静电性场强为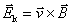 ,方向由 ,方向由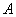 指向 指向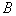 (图9-9),其大小为 (图9-9),其大小为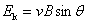 ;同样,在 ;同样,在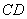 段中, 段中,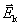 的方向由 的方向由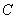 指向 指向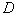 ,大小和 ,大小和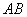 段中的相等;在 段中的相等;在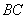 和 和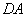 段中, 段中,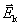 的方向都垂直于线段。如设 的方向都垂直于线段。如设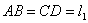 , ,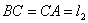 ,则 ,则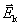 沿 沿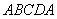 的线积分,即在线圈中的动生电动势为 的线积分,即在线圈中的动生电动势为
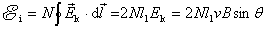
线圈绕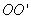 轴转动时,从图中可知, 轴转动时,从图中可知,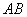 和 和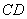 段的速度 段的速度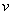 与角速度 与角速度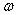 的关系为 的关系为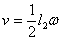 ,代入上式中则有 ,代入上式中则有
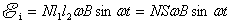
式中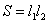 是矩形线圈的面积,结果和式(9-9)相同。 是矩形线圈的面积,结果和式(9-9)相同。
4.关于动生电动势的进一步讨论
我们从安培力作功、电路的欧姆定律及能量守恒的观点来分析下面的例子。
在图9-11的电路中,由一个电动势为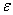 的电源在电路中产生电流 的电源在电路中产生电流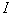 。垂直纸面向里的磁场 。垂直纸面向里的磁场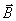 ,对长为 ,对长为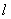 载流导线 载流导线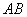 段施以安培力 段施以安培力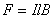 ,使 ,使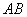 段导线无摩擦地向右滑动。在 段导线无摩擦地向右滑动。在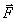 的作用下,在 的作用下,在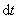 时间内,导线沿力 时间内,导线沿力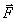 的方向移动 的方向移动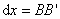 距离至 距离至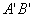 位置,故在 位置,故在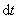 时间内,安培力 时间内,安培力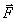 对载流导线 对载流导线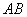 所作的功为 所作的功为
用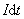 除上式,经移项得 除上式,经移项得
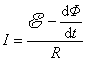
从全电路欧姆定律的观点来看,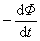 在电路中的作用和电源电动势处于同等地位,它就是由磁通量变化所引起的感应电动势,即法拉第电磁感应定律 在电路中的作用和电源电动势处于同等地位,它就是由磁通量变化所引起的感应电动势,即法拉第电磁感应定律
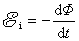
这样,就由能量守恒定律导出了电磁感应定律,说明磁力作功是和电磁感应有内在联系的。在这里,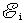 是导线 是导线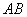 以速度 以速度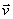 右运动的同时在导线中产生的动生电动势,其大小 右运动的同时在导线中产生的动生电动势,其大小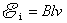 ,方向从 ,方向从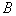 指向 指向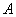 。在电路中,这个动生电动势 。在电路中,这个动生电动势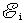 与电源的电动势 与电源的电动势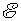 有相反的指向,这时电源处于供应电能的地位,“运动导线 有相反的指向,这时电源处于供应电能的地位,“运动导线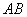 ”反而处于接受电能的地位,所以通常把 ”反而处于接受电能的地位,所以通常把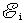 称为反电动势。我们在习惯上常说,电源 称为反电动势。我们在习惯上常说,电源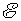 要克服反电动势 要克服反电动势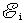 而作功。 而作功。
通过计算我们可以看到,电源为克服反电动势而用去的电能等于
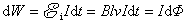
这正好和磁力所作的功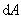 相等。实质上我们这里讨论的就是电动机的工作原理,电动机输出的机械能就是来自电能的转化,我们所说的“克服反电动势而消耗了电能”和“磁力作正功而输出机械能”就是电动机中“电能向机械能转化”同一事实的两种不同的表述。 相等。实质上我们这里讨论的就是电动机的工作原理,电动机输出的机械能就是来自电能的转化,我们所说的“克服反电动势而消耗了电能”和“磁力作正功而输出机械能”就是电动机中“电能向机械能转化”同一事实的两种不同的表述。
最后,对于电动机中反电动势的问题再指出一点,电动机在工作时,电枢线圈两端就产生反电动势。在启动时,由于电枢转动较慢,反电动势较小,线圈中就有很大的起动电流。当电动机的转速增加时,由于反电动势增加,电流就减小。所以在直流电动机起动时,常用电阻和电枢线圈串联或用其他方法以限制起动电流,当转速增加到一定大小时,反电动势已足够大,这时再撤去电阻。 |






