1. 电路中的能量转化 电路中的能量转化
在第七章中我们讨论过,在形成带电系统的过程中,外力必须克服静电场力而作功,根据功能原理,外界作功所消耗的能量最后转化为电荷系统或电场的能量,电场的能量密度为
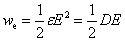
同样,在回路系统中通以电流时,由于各回路的自感和回路之间互感的作用,回路中的电流要经历一个从零到稳定值的暂态过程,在这个过程中,电源必须提供能量用来克服自感电动势及互感电动势而作功,最后转化为载流回路的能量和回路电流间的相互作用能,也就是磁场的能量。
我们仍以图9-22所示的简单回路为例,讨论回路中电流增长过程中能量的转化情况。设电路接通后回路中某瞬时的电流为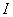 ,自感电动势为 ,自感电动势为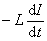 ,由欧姆定律得 ,由欧姆定律得
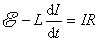
如果从 开始,经一足够长的时间 开始,经一足够长的时间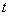 ,可以认为回路中的电流已从零增长到稳定值 ,可以认为回路中的电流已从零增长到稳定值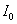 ,则在这段时间内电源电动势所作的功为 ,则在这段时间内电源电动势所作的功为
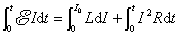
在自感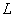 和电流无关的情况下,上式化为 和电流无关的情况下,上式化为
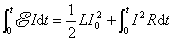
式中 是 是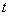 时间内电源提供的部分能量转化为消耗在电阻上的焦耳-楞次热; 时间内电源提供的部分能量转化为消耗在电阻上的焦耳-楞次热;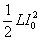 项是回路中建立电流的暂态过程中电源电动势克服自感电动势所作的功,这部分功转化为载流回路的能量。由于在回路中形成电流的同时,在回路周围空间也建立了磁场,显然,这部分能量也就是储存在磁场中的能量。当回路中的电流达到稳定值 项是回路中建立电流的暂态过程中电源电动势克服自感电动势所作的功,这部分功转化为载流回路的能量。由于在回路中形成电流的同时,在回路周围空间也建立了磁场,显然,这部分能量也就是储存在磁场中的能量。当回路中的电流达到稳定值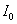 后,断开 后,断开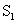 ,并同时接通 ,并同时接通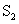 ,这时回路中的电流按指数规律 ,这时回路中的电流按指数规律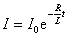 衰减,此电流通过 衰减,此电流通过 时,放出的焦耳-楞次热为 时,放出的焦耳-楞次热为

这表明随着电流衰减引起的磁场消失,原来储存在磁场中的能量又反馈到回路中以热的形式全部释放出来,这也说明了磁场具有能量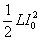 的推断是正确的。因此可知,一个自感为 的推断是正确的。因此可知,一个自感为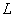 的回路,当其中通有电流 的回路,当其中通有电流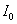 时,其周围空间磁场的能量为 时,其周围空间磁场的能量为
式中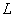 的单位用 的单位用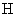 , ,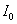 的单位用 的单位用 ,则 ,则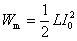 的单位为 的单位为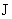 。 。
式(9-25)是用线圈的自感及其中电流表示的磁能,经过变换,磁能也可用描述磁场本身的量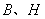 来表示。 来表示。
2.磁场的能量密度
为了简单起见,考虑一个很长的直螺线管,管内充满磁导率为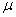 的均匀磁介质。当螺线管通一有电流 的均匀磁介质。当螺线管通一有电流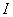 时,管中磁场近似看做均匀,而且把磁场看做全部集中在管内。由上一章讨论可知螺线管内的磁感应强度 时,管中磁场近似看做均匀,而且把磁场看做全部集中在管内。由上一章讨论可知螺线管内的磁感应强度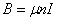 ,它的自感 ,它的自感 ,式中 ,式中 为螺线管单位长度的匝数, 为螺线管单位长度的匝数, 为螺线管内磁场空间的体积。把 为螺线管内磁场空间的体积。把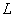 及 及 代入式(9-25),得到磁能的另一表示式 代入式(9-25),得到磁能的另一表示式
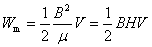
而磁场能量密度是
上述磁场能量密度的公式虽是从螺线管中均匀磁场的特例导出的,但它是适用于各种类型磁场的普遍公式。公式说明,在任何磁场中,某一点的磁场能量密度,只与该点的磁感应强度 及介质的性质有关,这也说明了磁能是定域在磁场中的这个客观事实。 及介质的性质有关,这也说明了磁能是定域在磁场中的这个客观事实。
如果知道磁场能量密度及均匀磁场所占的空间,可用上式计算出磁场的总磁能。倘若磁场是不均匀的,那么可以把磁场划分为无数体积元 在每个小体积内,磁场可以看做是均匀的,因此式(9-26)就能表示这些体积元内的磁场能量密度,于是体积为 在每个小体积内,磁场可以看做是均匀的,因此式(9-26)就能表示这些体积元内的磁场能量密度,于是体积为 内的磁场能量为 内的磁场能量为
对整个磁场不为零的空间积分,即得磁场的总能量为
另外,因为式(9-25)和式(9-28)是相等的,所以
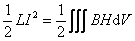
如果能求出电流回路的磁场能量,根据此式就可求出回路的自感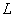 。 。
|