1.同一直线上两个同频率的简谐振动的合成
在实际问题中,常会遇到一个质点同时参与几个振动的情况。例如,当两个声波同时传到某一点时,该点处的空气质点就同时参与两个振动。根据运动叠加原理,这时质点所作的运动实际上就这两个振动的合成。一般的振动合成问题比较复杂,我们只讨论几种简单情况。
设一质点在一直线上同时进行两个独立的同频率(亦即角频率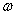 相同)的简谐振动。如果取这一直线为 相同)的简谐振动。如果取这一直线为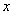 轴,以质点的平衡位置为原点,在任一时刻 轴,以质点的平衡位置为原点,在任一时刻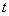 ,这两个振动的位移分别为: ,这两个振动的位移分别为:
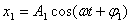
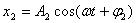
式中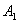 、 、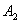 和 和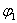 、 、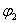 分别表示两个振动的振幅和初相位。既然 分别表示两个振动的振幅和初相位。既然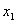 和 和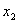 都是表示在同一直线方向上、距同一平衡位置的位移,所以合位移 都是表示在同一直线方向上、距同一平衡位置的位移,所以合位移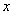 仍在同一直线上,而为上述两个位移的代数和,即: 仍在同一直线上,而为上述两个位移的代数和,即:
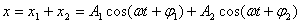
应用三角函数的等式关系可以将上式化成:
式中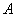 和 和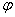 的值分别为: 的值分别为:
这说明合振动仍是简谐振动,其振动方向和频率都与原来的两个振动相同。
应用旋转振幅矢量图,可以很方便地得到上述两简谐振动的合振动。
现在来讨论振动合成的结果。从式(10-43a)可以看出,合振动的振幅与原来的两个振动的相位差(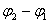 )有关。下面讨论两个特例,将来在研究声、光等波动过程的干涉和衍射现象时,这两个特例常要用到。 )有关。下面讨论两个特例,将来在研究声、光等波动过程的干涉和衍射现象时,这两个特例常要用到。
2.同一直线上两个不同频率的简谐振动的合成
如果两个同方两简谐振动的频率并不相同,而在矢量图示法中,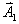 和 和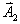 转动速度就不相同。这样, 转动速度就不相同。这样,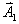 和 和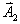 的相位差将随着时间而改变。这时,合矢量 的相位差将随着时间而改变。这时,合矢量 的长度和角速度都将随时间而改变。合矢量 的长度和角速度都将随时间而改变。合矢量 所代表的合振动虽然仍与原来振动的方向相同,但不再是简谐振动,而是比较复杂的运动。研究频率相近的两个振动的合成情况,在实用上颇为重要。这时,合振动具有特殊的性质,合振动的振幅随时间发生周期性的变化,这种现象称为拍。我们可用演示实验来证实这种现象。取两支频率相同的音叉,在一个音叉上套上一个小铁圈,使它的频率有很小的变化。分别敲击这两支音叉,我们听到的声强是均匀的;如果同时敲击音叉,结果听到“嗡”、“嗡”、“嗡”……的声音,反映出合振动的振幅存在时强时弱的周期性变化,这就是拍的现象。 所代表的合振动虽然仍与原来振动的方向相同,但不再是简谐振动,而是比较复杂的运动。研究频率相近的两个振动的合成情况,在实用上颇为重要。这时,合振动具有特殊的性质,合振动的振幅随时间发生周期性的变化,这种现象称为拍。我们可用演示实验来证实这种现象。取两支频率相同的音叉,在一个音叉上套上一个小铁圈,使它的频率有很小的变化。分别敲击这两支音叉,我们听到的声强是均匀的;如果同时敲击音叉,结果听到“嗡”、“嗡”、“嗡”……的声音,反映出合振动的振幅存在时强时弱的周期性变化,这就是拍的现象。
我们把这两个简谐振动(设它们的角频率很接近,分别为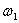 和 和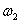 ,且( ,且(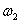 > >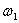 ,而初相相同)的振动方程写为: ,而初相相同)的振动方程写为:
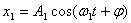
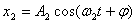
根据运动叠加原理,两者的合振动是:
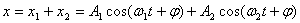
为方便计,设两者的振幅相等,即令 ,则上式可写成: ,则上式可写成:
在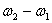 远小于 远小于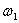 或 或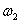 的情况,式中第一项因子随时间作缓慢地变化,第二项因子是角频率近于 的情况,式中第一项因子随时间作缓慢地变化,第二项因子是角频率近于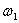 或 或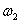 的简谐函数,因此合成运动可近似看做是角频率为 的简谐函数,因此合成运动可近似看做是角频率为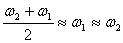 、振幅为 、振幅为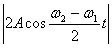 的简谐振动。由于振幅的缓慢变化是周期性的,所以振动出现时强时弱的拍现象。 的简谐振动。由于振幅的缓慢变化是周期性的,所以振动出现时强时弱的拍现象。 |
|
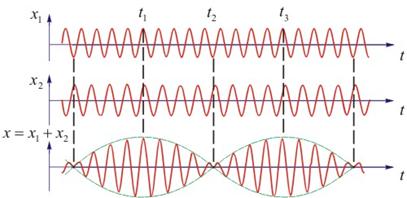
图 10-15  为周期,因而振幅变化周期 为周期,因而振幅变化周期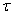 可由 可由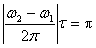 决定,故振幅变化的频率即拍频: 决定,故振幅变化的频率即拍频:
拍频的数值等于两分振动频率之差。
拍现象也可以从谐振动的旋转矢量合成图示法得到说明。
拍现象在技术上有重要应用。
|