例题10-5-1 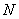 个同方向、同频率的简谐振动,它们的振幅相等,初相分别为 个同方向、同频率的简谐振动,它们的振幅相等,初相分别为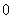 , ,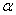 , ,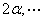 ,依次差一个常量 ,依次差一个常量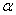 ,振动表达式可写为: ,振动表达式可写为:
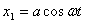
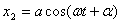
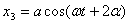
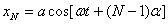
解:对这种情况,采用旋转矢量法,可以避免繁杂的三角函数运算,有很大的优越性。
按矢量合成法则,将每一简谐振动在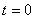 时刻的振幅矢量 时刻的振幅矢量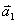 、 、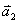 、 、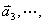 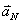 首尾相接,而相邻矢量的夹角均为 首尾相接,而相邻矢量的夹角均为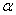 (如图)。它们构成正多边形的一部分。可见合振动的振幅矢量 (如图)。它们构成正多边形的一部分。可见合振动的振幅矢量 等于各分振动振幅矢量的矢量和。 等于各分振动振幅矢量的矢量和。
下面我们采用几何方法较方便地求出合振动振幅矢量的大小和方向。在图中作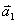 和 和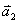 的垂直平分线,两者相交于 的垂直平分线,两者相交于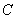 点,它们的夹角显然为 点,它们的夹角显然为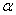 。而以 。而以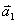 和 和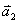 为底边,以 为底边,以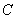 为顶点的三角形的顶角也等于 为顶点的三角形的顶角也等于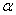 ,所以 ,所以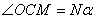 。因 。因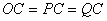 并令其等于 并令其等于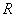 ,所以 ,所以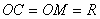 。从等腰三角形 。从等腰三角形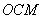 ,可以求得边长 ,可以求得边长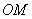 ,即合振幅矢量 ,即合振幅矢量 的大小为: 的大小为:
所以: 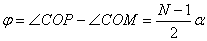
式中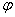 为 为 与 与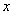 轴间的夹角,就是合振动的初相。 轴间的夹角,就是合振动的初相。
最后求得合振动的表达式为:

如果各分振动的初相相同,即 ,于是有: ,于是有:
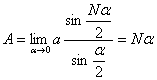
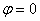
这时合振幅为最大值。 |