1.波动方程
把平面简谐波的波函数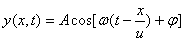 分别对 分别对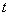 和 和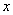 求二阶偏导数,得到 求二阶偏导数,得到
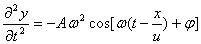
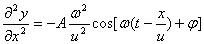
比较上列两式,即得
如果从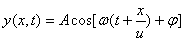 出发,所得的结果完全相同,仍是式(11-5)。任一平面波,如果不是简谐波,也可认为是许多不同频率的平面余弦波的合成,在对 出发,所得的结果完全相同,仍是式(11-5)。任一平面波,如果不是简谐波,也可认为是许多不同频率的平面余弦波的合成,在对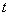 和 和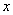 偏微分两次后,所得的结果将仍是式(11-5)。所以式(11-5)反映一切平面波的共同特征,称为平面波的波动方程。 偏微分两次后,所得的结果将仍是式(11-5)。所以式(11-5)反映一切平面波的共同特征,称为平面波的波动方程。
2.波动方程的建立
我们可以进一步从动力学的观点,更本质地分析波动方程的意义,下面以平面纵波在固体细长棒中的传播为例进行分析。
设有截面为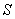 、密度为 、密度为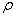 的固体细长棒(图11-8)。假定有平面纵波沿着棒长方向传播,棒中的每一小段将不断地受到拉伸和压缩。观察一个体积元 的固体细长棒(图11-8)。假定有平面纵波沿着棒长方向传播,棒中的每一小段将不断地受到拉伸和压缩。观察一个体积元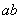 ,其原长度为 ,其原长度为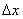 ,体积为 ,体积为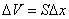 ,如果在某一时刻这体积元正在被拉长,左端面处的胁强为 ,如果在某一时刻这体积元正在被拉长,左端面处的胁强为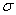 (受力方向左),右端面的胁强将为 (受力方向左),右端面的胁强将为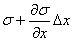 (受力方向向右),式中的 (受力方向向右),式中的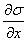 表示这时刻胁强随距离的改变率。因此体积元所受到的合力是 表示这时刻胁强随距离的改变率。因此体积元所受到的合力是
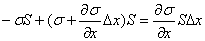
已知体积元的质量为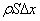 ,如振动速度为 ,如振动速度为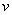 ,对体积元应用牛顿第二定律,即得 ,对体积元应用牛顿第二定律,即得
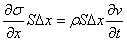
或 |
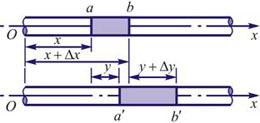
图11-8 |
由于体积元左端的位移为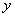 ,右端的位移为 ,右端的位移为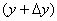 。因此体积元的长度变化为 。因此体积元的长度变化为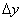 ,体积元的原长为 ,体积元的原长为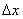 ,所以胁变为 ,所以胁变为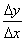 或 或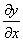 。根据胡克定律,以 。根据胡克定律,以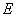 代表杨氏模量,即得 代表杨氏模量,即得
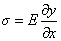 ; ;
又因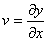 ,牛顿第二定律的方程就变为如下偏微分方程 ,牛顿第二定律的方程就变为如下偏微分方程
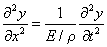
上式表示棒中各点振动的位移所满足的微分方程,式中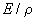 是一个常量,这偏微分方程称为细棒中平面纵波的波动方程。如将平面简谐波的表式 是一个常量,这偏微分方程称为细棒中平面纵波的波动方程。如将平面简谐波的表式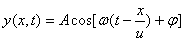 求导后代入方程后可知,当 求导后代入方程后可知,当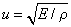 等式成立。因此在固体细长棒中传播的纵波的波速为 等式成立。因此在固体细长棒中传播的纵波的波速为
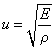
由此我们得到与式(11-5)相同的微分方程
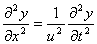
而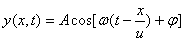 就是波动方程的解。 就是波动方程的解。
按照偏微分方程理论,上述方程的一般解答是
式中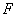 和 和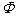 代表两个任意周期性函数。很容易看出,这一解既包括沿 代表两个任意周期性函数。很容易看出,这一解既包括沿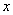 轴正向传播的波,也包括负向传播的波,而且还不仅限于余弦波。 轴正向传播的波,也包括负向传播的波,而且还不仅限于余弦波。
3.波的传播速度
波的传播速度简称波速,就是波阵面沿波线的推进速度(也称为相速度)。
波的传播速度决定于介质的特性,例如,弹性波的传播速度决定于介质的惯性与弹性。具体地说,就是决定于介质的密度和弹性模量。
液体和气体只有体变弹性,在液体和气体内部就只能传播与体变有关的弹性纵波。理论证明在液体和气体中纵波传播速度为
式中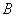 是介质的体变弹性模量, 是介质的体变弹性模量,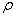 是介质的密度。对于理想气体,根据分子动理论和热力学,可推出声速公式为
式中 是介质的密度。对于理想气体,根据分子动理论和热力学,可推出声速公式为
式中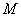 是气体的摩尔质量, 是气体的摩尔质量,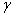 是气体的比热容比, 是气体的比热容比,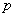 是气体的压强, 是气体的压强,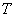 是热力学温度, 是热力学温度,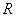 是摩尔气体常量。 是摩尔气体常量。
液体的表面可出现由重力和表面张力所引起的表面波。这是一种由纵波和横波叠加的波,传播速度决定于重力加速度和表面张力系数,液体表面波波速的普遍式为
其中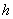 是液体的深度, 是液体的深度,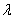 是波长, 是波长,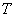 是表面张力系数, 是表面张力系数,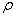 是液体的密度, 是液体的密度,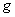 是重力加速度, 是重力加速度,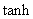 是双曲正切函数,若不考虑表面张力,对于水深 是双曲正切函数,若不考虑表面张力,对于水深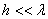 的浅水波 的浅水波
对于深水波
固体中能够产生切变、体变、长变等各种弹性变形,所以在固体中既能传播与切变有关的横波又能传播与体变或长变有关的纵波。在固体中,横波和纵波的传播速度可分别用下列两式计算
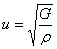 (横波) |
(11-13) |
|
(11-14) |
式中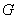 和 和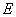 分别为介质的切变模量和杨氏模量。 分别为介质的切变模量和杨氏模量。
柔软绳索和弦线中横波的传播速度为
式中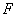 为绳索或弦线中的张力, 为绳索或弦线中的张力,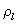 为绳索或弦线单位长度的质量。 为绳索或弦线单位长度的质量。 |