在波动光学中,我们研究了光的干涉、衍射等现象,这些现象证实了光的波动性。在讨论热辐射、光电效应和康普顿效应等现象中,普朗克和爱因斯坦关于光的微粒性理论又取得了极大的成功。这样,为了解释光的全部现象,我们不得不承认光的本性具有“波粒二象性”。正是表式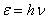 和 和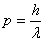 把标志波动性质的 把标志波动性质的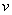 和 和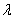 和标志微粒性的 和标志微粒性的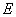 和 和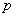 ,通过普朗克常量 ,通过普朗克常量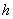 定量地联系起来了。 定量地联系起来了。
1924年年轻的博士研究生德布罗意在光的波粒二象性的启发下,从自然界的对称性出发,提出了与光的波粒二象性完全对称的设想,即实物粒子(如电子、质子等)也具有波粒二象性的假设。他认为,“整个世纪以来(指19世纪),在光学中,比起波动的研究方法来,如果说是过于忽视了粒子的研究方法的话,那么在实物的理论中,是否发生了相反的错误呢?是不是我们把粒子的图像想得太多,而过分地忽略了波的图像呢?”他还注意到几何光学与经典力学的相似性,根据类比的方法,提出了实物粒子也具有波动性的假设。
德布罗意认为,质量为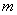 的粒子、以速度 的粒子、以速度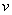 匀速运动时,具有能量 匀速运动时,具有能量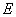 和动量 和动量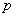 ;从波动性方面来看,它具有波长 ;从波动性方面来看,它具有波长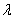 和频率 和频率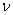 ,而这些量之间的关系也和光波的波长、频率与光子的能量、动量之间的关系一样,应遵从下述公式 ,而这些量之间的关系也和光波的波长、频率与光子的能量、动量之间的关系一样,应遵从下述公式
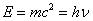 |
(13-29) |
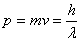 |
(13-30) |
所以对具有静止质量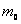 的实物粒子来说,若粒子以速度 的实物粒子来说,若粒子以速度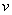 运动,则该粒子所表现的平面单色波的波长是 运动,则该粒子所表现的平面单色波的波长是
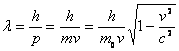 |
(13-31) |
式(13-31)称为德布罗意公式。人们通常把这种物质所表现的波称为德布罗意波。薛定谔在诠释波的物理意义时,把这种波称为物质波。如果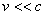 ,那么 ,那么
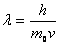 |
(13-32) |
以电子为例,用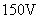 的电势差所加速的电子,德布罗意波长等于 的电势差所加速的电子,德布罗意波长等于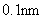 ,与X射线的波长同数量级;而当 ,与X射线的波长同数量级;而当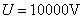 时, 时, 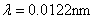 ,所以德布罗意波长是很短的。 ,所以德布罗意波长是很短的。
德布罗意的物质波概念成功地解释了玻尔氢原子假设中令人困惑的电子轨道角动量量子化的条件。
德布罗意的导师朗之万(P.Laugevin)把德布罗意的论文寄给爱因斯坦,爱因斯坦称赞德布罗意的论文“揭开了自然界巨大帷幕的一角”,“看来疯狂,可真是站得住脚呢”。由于德布罗意提出电子的波动性,荣获1929年诺贝尔物理学奖。 |