要确定一个宏观物体的运动状态,可以同时指出它在某一时刻的位置和速度(或动量)。牛顿运动方程(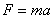 )就是描述宏观物体运动的普遍方程。但对微观粒子而言,由于其具有波粒二象性,所以它和宏观物体运动具有质的差别。那么微观粒子的运动状态是如何描述的呢?微观粒子的运动方程又是怎样的呢? 薛定谔首先用物质波波函数来描写微观粒子的运动状态,然后建立反映微观粒子运动的基本方程——薛定谔方程。 )就是描述宏观物体运动的普遍方程。但对微观粒子而言,由于其具有波粒二象性,所以它和宏观物体运动具有质的差别。那么微观粒子的运动状态是如何描述的呢?微观粒子的运动方程又是怎样的呢? 薛定谔首先用物质波波函数来描写微观粒子的运动状态,然后建立反映微观粒子运动的基本方程——薛定谔方程。
前面曾指出具有能量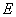 和动量 和动量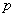 的自由运动的一个微观粒子,必然同时表现波动性。因此,我们不能像经典物理那样,确定这个自由粒子在某一时刻的位置,而需要用波函数描述它的状态。自由粒子的能量 的自由运动的一个微观粒子,必然同时表现波动性。因此,我们不能像经典物理那样,确定这个自由粒子在某一时刻的位置,而需要用波函数描述它的状态。自由粒子的能量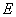 和动量 和动量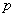 都是常量,所以自由粒子的物质波的频率和波长也都不变。我们知道,频率为 都是常量,所以自由粒子的物质波的频率和波长也都不变。我们知道,频率为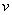 、波长为 、波长为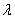 、沿x轴方向传播的平面波可以用下式表示: 、沿x轴方向传播的平面波可以用下式表示:
或将这个公式写成复数形式
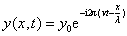 |
|
而只取其实数部分。如将关系式(13-30)和式(13-31)代入上式,我们便得到自由粒子的平面波,或者说,描写自由粒子波动性的平面物质波为
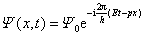 |
(13-38) |
为了和一般波动区别开来,在式中用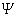 代表 代表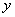 。式(13-38)便是描述能量为 。式(13-38)便是描述能量为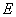 、动量为 、动量为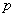 沿 沿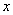 方向运动的自由粒子的德布罗意波,并称 方向运动的自由粒子的德布罗意波,并称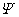 为物质波的波函数。 为物质波的波函数。
现在,我们用光波与物质波对比的方法来阐明波函数的物理意义。从波动的观点来看,光的衍射图样亮处光强大,暗处光强小。而光强与光振动的振幅平方成正比,所以图样亮处光振动的振幅平方大,暗处的光振动的振幅平方小。但从微粒的观点来看,光强大的地方表示单位时间内到达该处的光子数多,光强小的地方,则表示单位时间内到达该处的光子数少。或从统计观点来看,这就相当于光子到达亮处的概率要远大于光子到达暗处的概率。因为这两种看法是等效的,所以结论是,光子在某处附近出现的概率与该处的光强成正比,也就是与该处光振动的振幅的平方成正比。
电子的衍射图样和光的衍射图样相类似,对电子及其他微观粒子来说,在微粒性与波动性之间,也应有类似的结论。即物质波的强度也应与波函数的平方成正比,物质波强度较大的地方,也就是粒子分布较多的地方。粒子在空间某处分布数目的多少,与单个粒子在该处出现的概率成正比。因此,得到类似的结论:在某一时刻,在空间某一地点,粒子出现的概率正比于该时刻、该地点的波函数的平方。这是玻恩(M.Born)提出的波函数的统计诠释。因此,德布罗意波(或物质波)既不同于机械波,也不同于电磁波,而是一种体现微观粒子运动的概率波。由波函数的统计诠释可以看出,对微观粒子讨论运动的轨道是没有意义的,因为反映出来的只是微观粒子运动的统计规律,这与宏观物体的运动有着本质的差别。下面,我们用电子双缝干涉实验来具体说明概率波的含义。
在电子双缝干涉实验中,如果入射电子流的强度大,即单位时间内有很多电子通过双缝,则底片上出现一般的干涉图样。然而,如果入射电子流强度很小,电子几乎是一个一个地通过双缝,这时底片上就会出现一个一个的点,显示出电子的粒子性,它们是随机分布的,但总是落在干涉条纹所在的位置上,随着时间的延长,电子数目逐渐增多,它们在底片上的分布就逐渐形成了干涉图样,显示出了电子的波动性。由此可见,电子在底片上各处出现的概率具有一定的分布。图13-23给出了1989年日本物理学家外村彰(A. Tonomura)等所做的电子双缝干涉实验在不同的“曝光”时间下记录到的电子的位置分布图。

图13-23 电子双缝干涉图像
[电子束大约1000个/s通过双缝,曝光时间(a)0.01s;(b)0.1s;(c)3s;(d)20s;(e)70s]
|
在一般情况下,物质波的波函数是复数,而概率却必须是正实数,所以,在某一时刻空间某一地点粒子出现的概率正比于波函数与其共轭复数的乘积,即 。在空间某点 。在空间某点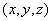 附近找到粒子的概率与这区域的大小有关,在一个很小的区域 附近找到粒子的概率与这区域的大小有关,在一个很小的区域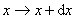 , ,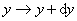 , ,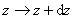 范围内, 范围内,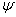 可以认为不变,粒子在该区域内出现的概率将正比于体积元 可以认为不变,粒子在该区域内出现的概率将正比于体积元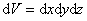 的大小,而为 的大小,而为
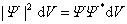 |
(13-39) |
式中 表示在某一时刻在某点处单位体积内粒子出现的概率,称为概率密度 。一定时刻在空间给定的体积元 表示在某一时刻在某点处单位体积内粒子出现的概率,称为概率密度 。一定时刻在空间给定的体积元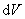 内出现粒子的概率应有一定的量值,不可能既是这个量值又为那个量值,因此波函数 内出现粒子的概率应有一定的量值,不可能既是这个量值又为那个量值,因此波函数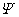 必须是单值函数。又因为整个空间内出现粒子的总概率等于1,所以将式(13-39)对整个空间积分后,应有 必须是单值函数。又因为整个空间内出现粒子的总概率等于1,所以将式(13-39)对整个空间积分后,应有
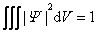 |
(13-40) |
上式称为归一化条件。
综上所述,在量子力学中,用来描写微观粒子的状态的波函数是时间和空间的单值函数。空间某点波函数的模的平方表示粒子在该点附近出现的概率。根据对波函数的统计诠释,必须要求波函数是单值、连续、有限而且是归一化的函数。
波函数的统计诠释是玻恩在1929年提出来的,为此,他获得了1954年诺贝尔物理学奖。
|