总结前面的讨论,原子中电子的状态应由下列四个量子数来确定:
(1) 主量子数n:n=1,2,3,…。主量子数n可以大体上决定原子中电子的能量。
(2) 角量子数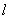 : : ,1,2,…,(n-1)。角量子数可以决定电子轨道角动量。一般说来,处于同一主量子数 ,1,2,…,(n-1)。角量子数可以决定电子轨道角动量。一般说来,处于同一主量子数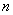 而不同角量子数 而不同角量子数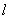 的状态中的电子,其能量稍有不同。 的状态中的电子,其能量稍有不同。
(3) 磁量子数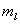 : :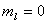 ,±1,±2,…,± ,±1,±2,…,±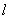 。磁量子数可以决定轨道角动量在外磁场方向上的分量。 。磁量子数可以决定轨道角动量在外磁场方向上的分量。
(4) 自旋磁量子数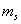 : :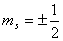 。自旋磁量子数决定电子自旋角动量在外磁场方向上的分量。 。自旋磁量子数决定电子自旋角动量在外磁场方向上的分量。
下面将根据四个量子数对原子中电子运动状态的限制,来确定原子核外电子的分布情况。
电子在原子中的分布遵从下列两个原理:
(1) 泡利不相容原理
原子内电子的状态由四个量子数n、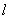 、 、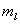 、 、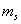 来确定,在一个原子系统内,不可能有两个或两个以上的电子具有相同的状态,亦即不可能具有相同的四个量子数。 来确定,在一个原子系统内,不可能有两个或两个以上的电子具有相同的状态,亦即不可能具有相同的四个量子数。
当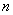 给定时, 给定时,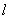 的可能值为0,1,…, 的可能值为0,1,…,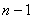 共 共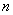 个;当 个;当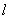 给定时, 给定时,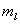 的可能值为 的可能值为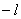 , ,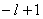 ,…,0,…、 ,…,0,…、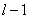 、 、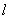 ,共 ,共 个;当 个;当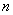 、 、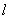 、 、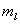 都给定时, 都给定时,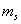 取 取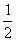 和 和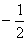 两个可能值。所以,根据泡利不相容原理可以算出,原子中具有相同主量子数 两个可能值。所以,根据泡利不相容原理可以算出,原子中具有相同主量子数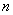 的电子数目最多为 的电子数目最多为
 |
(13-68) |
1916年,柯塞耳(W.Kossel)认为绕核运动的电子组成许多壳层,主量子数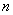 相同的电子属于同一壳层。 相同的电子属于同一壳层。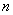 相同,不同的 相同,不同的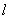 ,组成了分壳层,对应于 ,组成了分壳层,对应于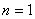 ,2,3,…的壳层分别用K,L,M,N,O,P,…来表示。可见当 ,2,3,…的壳层分别用K,L,M,N,O,P,…来表示。可见当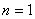 而 而 时,K壳层上可能有两个电子(s电子),以 时,K壳层上可能有两个电子(s电子),以 表示;又当 表示;又当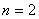 而 而 时(L壳层,s分层),可能有两个电子(s电子),以 时(L壳层,s分层),可能有两个电子(s电子),以 表示;再当 表示;再当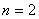 而 而 时(L壳层,p分层),可能有6个电子(p电子),以 时(L壳层,p分层),可能有6个电子(p电子),以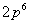 表示;所以L壳层上最多可能有8个电子,其余类推。表13-4列出原子内主量子数 表示;所以L壳层上最多可能有8个电子,其余类推。表13-4列出原子内主量子数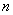 的壳层上最多可能有的电子数 的壳层上最多可能有的电子数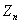 和具有相同 和具有相同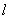 的分层上最多可能有的电子数。 的分层上最多可能有的电子数。
(2) 能量最小原理
原子系统处于正常状态时,每个电子趋向占有最低的能级。
能级基本上决定于主量子数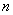 , ,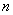 愈小,能级也愈低。所以离核最近的壳层,一般首先被电子填满。但能级也和角量子数 愈小,能级也愈低。所以离核最近的壳层,一般首先被电子填满。但能级也和角量子数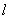 有关。因而在某些情况下,n较小的壳层尚未填满,而 有关。因而在某些情况下,n较小的壳层尚未填满,而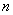 较大的壳层上却开始有电子填入了。这一情况在周期表的第四个周期中就开始表现出来。关于 较大的壳层上却开始有电子填入了。这一情况在周期表的第四个周期中就开始表现出来。关于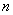 和 和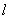 都不同的状态的能级高低问题,我国科学家徐光宪总结出这样的规律,即对于原子的外层电子而言,能级高低以 都不同的状态的能级高低问题,我国科学家徐光宪总结出这样的规律,即对于原子的外层电子而言,能级高低以 值来确定,该值越大,能级就愈高。例如, 值来确定,该值越大,能级就愈高。例如,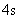 和 和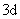 两个状态, 两个状态,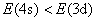 , ,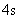 态应比 态应比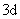 态先为电子所占有。 态先为电子所占有。
原子中电子按壳层排布参见表13-5。
|