1.波的叠加原理
几个波源产生的波,同时在一介质中传播,如果这几列波在空间某点处相遇,那么每一列波都将独立地保持自己原有的特性(频率、波长、振动方向等)传播,就像在各自的路程中,并没有遇到其他波一样,这称为波传播的独立性。在波传播相遇的区域内,任一点处质点的振动为各列波单独在该点引起的振动的合振动,即在任一时刻,该点处质点的振动位移是各个波在该点所引起的位移的矢量和。这一规律称为波的叠加原理。
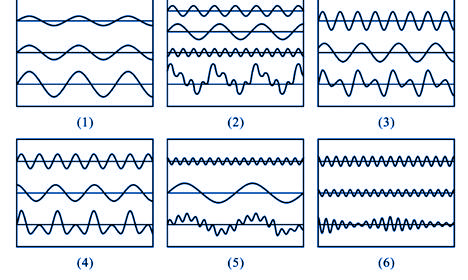
图11-21 两列(或两列以上)振动方向相同的同方向传播的波动的叠加 |
图11-21的各个图分别表示两列(或两列以上)振动方向相同的同方向传播的波动在不同条件下的叠加情况,每个图中最下面的图线表示叠加的结束。图11-21(1)表示同频率、不同振幅的两个波的叠加;图11-21(2)表示频率比为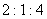 的三个不同振幅的波的叠加;图11-21(3)表示频率比为 的三个不同振幅的波的叠加;图11-21(3)表示频率比为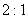 的两个等振幅波的叠加;图11-38(4)表示频率比为 的两个等振幅波的叠加;图11-38(4)表示频率比为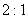 的两个等振幅波的叠加,与(3)有不同相位;图11-21(5)表示一个高频波和一个低频波的叠加;图11-21(6)表示频率相近的两个等幅波的叠加。 的两个等振幅波的叠加,与(3)有不同相位;图11-21(5)表示一个高频波和一个低频波的叠加;图11-21(6)表示频率相近的两个等幅波的叠加。
波的叠加原理在物理上的重要性,还在于可将下列复杂的波分解为简谐波的组合。事实上,这正如傅里叶所指出的:任何一质点的周期运动,都可用简谐振动的合成来表示一样。
2.波的干涉
一般地说,振幅、频率、相位等都不相同的几列波在某一点叠加时,情形是很复杂的。下面只讨论一种最简单而又最重要的情形,即两列频率相同、振动方向相同、相位相同或相位差恒定的简谐波的叠加。满足这些条件的两列波在空间任何一点相遇时,该点的两个分振动也有恒定相位差。但是对于空间不同的点,有着不同的恒定相位差。因而在空间某些点处,振动始终加强,而在另一些点处,振动始终减弱或完全抵消。这种现象称为干涉现象。能产生干涉现象的波称为相干波,相应的波源称为相干波源。
设有两列相干波在空间某点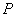 相遇,两列波叠加后的强度: 相遇,两列波叠加后的强度:
由于波的强度正比于振幅的平方,所以两列波叠加后的强度
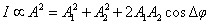
也就是
由此可知,叠加后波的强度随着两列相干波在空间各点所引起的振动相位差的不同而不同,就是说,空间各点的强度重新分布了,有些地方加强(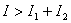 ),有些地方减弱( ),有些地方减弱(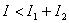 )。如果 )。如果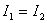 ,那么叠加后波的强度 ,那么叠加后波的强度
当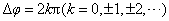 时,在这些位置波的强度最大,等于单个波强度的4倍( 时,在这些位置波的强度最大,等于单个波强度的4倍(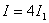 )。当 )。当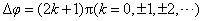 时,波的强度最小( 时,波的强度最小(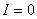 )。叠加后波的强度 )。叠加后波的强度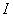 随相位差 随相位差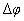 变化的情况如图11-22所示。 变化的情况如图11-22所示。
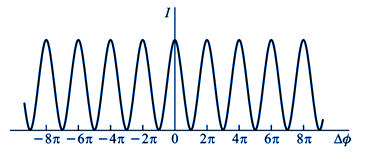
图11-22 |
|
应该指出,干涉现象是波动形式所独具的重要特征之一。因为只有波动的合成,才能产生干涉现象。干涉现象对于光学、声学等都非常重要,对于近代物理学的发展也有重大的作用。
3.驻波
现在来讨论俩两列振幅相同的相干波,在同一直线上,沿相反方向传播时所产生的叠加情形。为了产生横驻波可用图11-23所示的装置。音叉振动时,绳上产生波动,向右传播,达到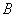 点时,在 点时,在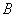 点反射,产生反射波向左传播。这样入射波和反射波在同一绳子上沿相反方向传播,它们将互相叠加。移动尖劈至适当位置,结果形成图上所示的波动状态。 点反射,产生反射波向左传播。这样入射波和反射波在同一绳子上沿相反方向传播,它们将互相叠加。移动尖劈至适当位置,结果形成图上所示的波动状态。
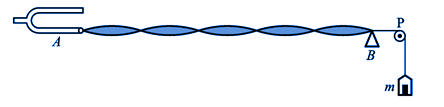
图11-23 |
从图上可以看出,由上述两列波叠加而成的波,从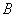 点开始被分成好几段,每段两端的点固定不动,而每段中的各质点则作振幅不同、相位相同的独立振动。中间的点,振幅最大,越靠近两端的点,振幅越小。而且还发现,相邻两段的振动方向是相反的。此时绳上各点,只有段与段之间的相位突变,而没有振动状态或相位的逐点传播,亦即没有什么“跑动”的波形,也没有什么能量向外传播,所以称这种波为驻波。驻波中始终静止不动的那些点称为波节,振幅最大的各点称为波腹。 点开始被分成好几段,每段两端的点固定不动,而每段中的各质点则作振幅不同、相位相同的独立振动。中间的点,振幅最大,越靠近两端的点,振幅越小。而且还发现,相邻两段的振动方向是相反的。此时绳上各点,只有段与段之间的相位突变,而没有振动状态或相位的逐点传播,亦即没有什么“跑动”的波形,也没有什么能量向外传播,所以称这种波为驻波。驻波中始终静止不动的那些点称为波节,振幅最大的各点称为波腹。
现在用简谐波的表式对驻波进行定量描述。为此,把沿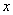 轴的正方向传播的波写为 轴的正方向传播的波写为
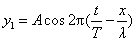
把沿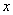 轴负方向传播的波写为 轴负方向传播的波写为
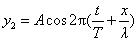
其合成波为
由上式可看出,合成以后各点都在作同周期的简谐振动,但各点的振幅为 ,即驻波的振幅与位置有关(与时间无关)。由此可以得到: ,即驻波的振幅与位置有关(与时间无关)。由此可以得到:
波腹、波节的位置
各点振动的相位
驻波的能量
在图11-23所示的实验中,反射点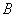 是固定不动的,在该处形成驻波的一个波节。这一结果说明,当反射点固定不动时,反射波与入射波在 是固定不动的,在该处形成驻波的一个波节。这一结果说明,当反射点固定不动时,反射波与入射波在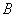 点是反相位的(图11-24a),如果反射波与入射波在 点是反相位的(图11-24a),如果反射波与入射波在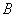 点是同相位的,那么合成的驻波在 点是同相位的,那么合成的驻波在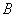 点应是波腹(图11-24b)。这就是说,当反射点固定不动时,反射波与入射波间有 点应是波腹(图11-24b)。这就是说,当反射点固定不动时,反射波与入射波间有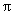 的相位突变。因为相距半波长的两点相位差为 的相位突变。因为相距半波长的两点相位差为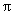 ,所以这个 ,所以这个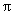 的相位突变一般形象化地称为“半波损失”。如反射点是自由的,合成的驻波在反射点将形成波腹,这时,反射波与入射波之间没有相位突变。 的相位突变一般形象化地称为“半波损失”。如反射点是自由的,合成的驻波在反射点将形成波腹,这时,反射波与入射波之间没有相位突变。
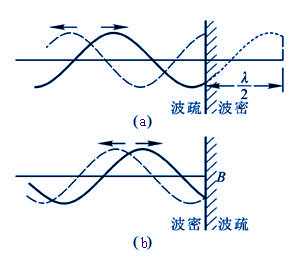
图11-24 |
|
4.弦线上的驻波
驻波现象有许多实际的应用。例如,弦线的两端拉紧固定(或细棒的两端固定),当拨动弦线时,弦线中就产生经两端反射而成的两列反向传播的波,叠加后形成驻波。由于在两固定端必须是波节,因而其波长有一定限制,波长与弦长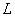 必须满足条件: 必须满足条件:
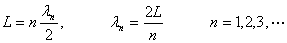
而波速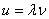 ,于是 ,于是
就是说,只有波长(或频率)满足上述条件的一系列波才能在弦上形成驻波。其中与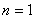 对应的频率称为基频,对弦来说, 对应的频率称为基频,对弦来说,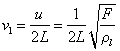 ,其他频率依次称为二次、三次…谐频(对声驻波则称为基音和泛音)(图11-25)。各种允许频率所对应的驻波(即简谐振动方式)即为简正模式,相应的频率为简正频率。对两端固定的弦,这一驻波系统,有无限多个简正模式和简正频率。一个系统的简正模式所对应的简正频率反映了系统的固有频率特性,如果外界驱使系统振动,当驱动力频率接近系统某一固有频率时,系统将被激发,产生振幅很大的驻波,这种现象也称为共振。 ,其他频率依次称为二次、三次…谐频(对声驻波则称为基音和泛音)(图11-25)。各种允许频率所对应的驻波(即简谐振动方式)即为简正模式,相应的频率为简正频率。对两端固定的弦,这一驻波系统,有无限多个简正模式和简正频率。一个系统的简正模式所对应的简正频率反映了系统的固有频率特性,如果外界驱使系统振动,当驱动力频率接近系统某一固有频率时,系统将被激发,产生振幅很大的驻波,这种现象也称为共振。
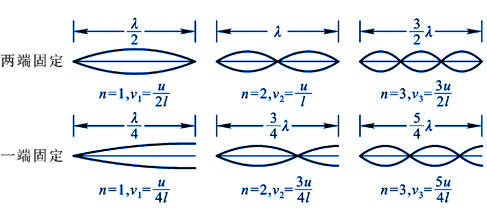
图11-25 |
对一端固定、一端自由的棒(或一端封闭、一端开放的管);或对两端自由的棒(或两端开放的管),也可作类似的分析,以确定它的简正模式(图11-25)。此外,锣面、鼓皮也都是驻波系统,由于是二维的情况,它们的简正模式要比棒的简正模式复杂得多。 |