若粒子在保守力场的作用下被限制在一定范围内运动,其势能曲线的形状与陷阱相似,故这种势能分布称为势阱。例如,电子在金属中的运动,质子在原子核中的势能曲线等。为了使计算简化,提出一个理想的势阱模型——无限深势阱。
设一维无限深势阱的势能分布如下:
其势能曲线如图13-25所示。
由于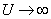 ,对于 ,对于 为有限值的粒子,要使上述方程成立,唯有 为有限值的粒子,要使上述方程成立,唯有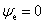 。 。
在阱内,设波函数为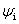 ,定态薛定谔方程为
令
于是方程可改写为 ,定态薛定谔方程为
令
于是方程可改写为
其解为
式中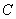 和 和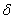 是两待定常数。因为在阱壁上波函数必须单值、连续,即应有
由此得
对波函数归一化,有
求得
于是得定态波函数 是两待定常数。因为在阱壁上波函数必须单值、连续,即应有
由此得
对波函数归一化,有
求得
于是得定态波函数
最后得波函数
我们将一维无限深势阱中粒子运动的特征总结如下:
粒子的最小能量状态称为基态,最小能量称为基态能。上式表明,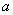 愈小, 愈小,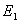 就愈大,粒子运动愈剧烈。按照经典理论,粒子的能量是连续分布的,其能量可以为零。但若能量为零,则动量必须为零,于是动量的不确定度 就愈大,粒子运动愈剧烈。按照经典理论,粒子的能量是连续分布的,其能量可以为零。但若能量为零,则动量必须为零,于是动量的不确定度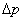 就不存在,根据不确定度关系,这只有 就不存在,根据不确定度关系,这只有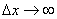 才有可能。实际上,粒子处于势阱中,它的 才有可能。实际上,粒子处于势阱中,它的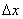 为势阱的宽度 为势阱的宽度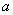 所限制,从而导致最小能量的出现。这种最小能量有时称为零点能。所以,零点能的存在与不确定度关系是协调一致的。许多实验证实了微观领域中能量量子化的分布规律,并证实了零点能的存在。 所限制,从而导致最小能量的出现。这种最小能量有时称为零点能。所以,零点能的存在与不确定度关系是协调一致的。许多实验证实了微观领域中能量量子化的分布规律,并证实了零点能的存在。
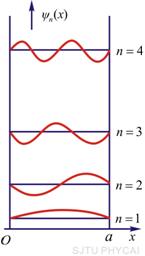
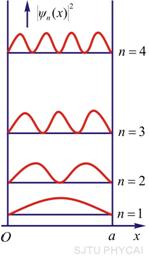
图13-27 势阱中的波函数和概率密度
|
(3)图13-27给出了势阱中粒子的波函数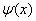 和粒子的概率密度 和粒子的概率密度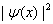 的分布曲线。从图中可以看出,粒子出现的概率是不均匀的。当 的分布曲线。从图中可以看出,粒子出现的概率是不均匀的。当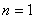 时,在 时,在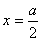 处粒子出现的概率最大;当 处粒子出现的概率最大;当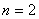 时,在 时,在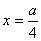 和 和 处概率最大;等等。概率密度的峰值个数和量子数 处概率最大;等等。概率密度的峰值个数和量子数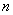 相等,这又和经典概念是很不同的。若是经典粒子,因为在势阱内不受力,粒子在两阱壁间作匀速直线运动,所以粒子出现的概率处处一样;对于微观粒子,只有当 相等,这又和经典概念是很不同的。若是经典粒子,因为在势阱内不受力,粒子在两阱壁间作匀速直线运动,所以粒子出现的概率处处一样;对于微观粒子,只有当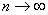 时,粒子出现的概率才是均匀的。 时,粒子出现的概率才是均匀的。
|