|
例题13-8-1 设想一电子在无限深势阱中运动,如果势阱宽度分别为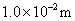 和 和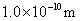 。试讨论这两种情况下相邻能级的能量差。 。试讨论这两种情况下相邻能级的能量差。
解: 根据势阱中的能量公式
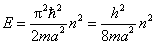
得到两相邻能级的能量差为
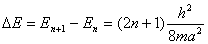
可见两相邻能级间的距离随着量子数的增加而增加,而且与粒子的质量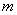 和势阱的宽度 和势阱的宽度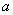 有关。 有关。
当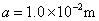 时 时

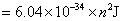
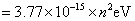
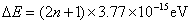
在这种情况下,相邻能级之间的距离是非常小的,我们可以把电子的能量看做是连续的。
当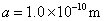 时 时
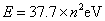
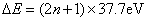
在这种情况下,相邻能级之间的距离是非常大的,这时电子能量的量子化就明显地表现出来。
由此可知,电子在小到原子尺度范围内运动时,能量的量子化特别显著。在普通尺度范围内运动时,能量的量子化就不显著,此时可以把粒子的能量看做是连续变化的。
当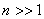 时,能级的相对间隔近似为 时,能级的相对间隔近似为
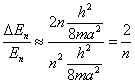
可见能级相对间隔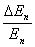 随着 随着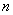 的增加成反比地减小。当 的增加成反比地减小。当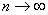 时, 时,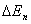 较之 较之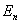 要小得多。这时,能量的量子化效应就不显著了,可认为能量是连续的,经典图样和量子图样趋于一致。所以,经典物理可以看做是量子物理中量子数 要小得多。这时,能量的量子化效应就不显著了,可认为能量是连续的,经典图样和量子图样趋于一致。所以,经典物理可以看做是量子物理中量子数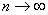 时的极限情况。 时的极限情况。 |